Page Not Found
Page not found. Your pixels are in another canvas.
Read moreA list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.
Page not found. Your pixels are in another canvas.
Read moreAbout me
Read moreI’ve switched the host of my blog to Ghost, so my blog is now located at https://bounded-regret.ghost.io/.
Feedly users can subscribe via RSS here. Or click the bottom-right subscribe button on this page to get e-mail notifications of new posts.
Read morePolarization caused by social media is seen by many as an important societal problem, which also overlaps with AI alignment (since social media recommendations come from ML algorithms). I have personally begun directing some of my research to recommender alignment, which has gotten me curious about the extent to which polarization is actually driven by social media. This blog post is the first in a series that summarizes my current take-aways. I’ll start (in this post) by looking at aggregate trends in polarization, then connect them with micro-level data on Facebook feeds in later posts.
I started out feeling that most polarization probably comes from social media. As I read more, my views have shifted: I think there’s pretty good evidence that other sources, including cable news, have historically driven a lot of polarization (see DellaVigna and Kaplan (2006) and Martin and Yurukoglu (2017)), and that we would be highly polarized even without social media. In addition, most readers of this post (and myself) are “extremely online”, and probably intuitively overestimate the impact of social media on a typical American. However, it is possible that social media has further accelerated polarization to an important degree, but the data are too noisy to provide strong evidence either way.
Read moreThere is a growing fear that algorithmic recommender systems, such as Facebook, Youtube, Netflix, and Amazon, are having negative effects on society, for instance by manipulating users into behaviors that they wouldn’t endorse (e.g. getting them addicted to feeds, leading them to form polarized opinions, recommending false but convincing content).
Some common responses to this fear are to advocate for privacy or to ask that users have greater agency over what they see. I argue below that neither of these will solve the problem, and that the problem may get far worse in the future. I then speculate on alternative solutions based on audits and “information marketplaces”, and discuss their limitations.
Read moreResearch ability, like most tasks, is a trainable skill. However, while PhD students and other researchers spend a lot of time doing research, we often don’t spend enough time training our research abilities in order to improve. For many researchers, aside from taking classes and reading papers, most of our training is implicit, through doing research and interacting with mentors (usually a single mentor–our PhD advisor or research manager). By analogy, we are like basketball players who somehow made it to the NBA, and are now hoping that simply playing basketball games will be enough to keep improving.
Drawing on this analogy, I want to talk about two habits that are ubiquitous among elite athletes, that have analogs in research that I feel are underutilized. Those who do pursue these habits as PhD students often improve quickly as researchers.
Read moreEach year I aim to donate around 10% of my income. In 2019, I fell behind on this, probably due to the chaos of COVID-19 (but really this was just an embarassing logistical failure on my part). I’ve recently, finally, finished processing donations for 2019 and 2020. In this post I write about my decisions, in case they are useful to others; see also here for a past write-up from 2016.
Read moreIn machine learning, we are obsessed with datasets and metrics: progress in areas as diverse as natural language understanding, object recognition, and reinforcement learning is tracked by numerical scores on agreed-upon benchmarks. Despite this, I think we focus too little on measurement—that is, on ways of extracting data from machine learning models that bears upon important hypotheses. This might sound paradoxical, since benchmarks are after all one way of measuring a model. However, benchmarks are a very narrow form of measurement, and I will argue below that trying to measure pretty much anything you can think of is a good mental move that is heavily underutilized in machine learning. I’ll argue this in three ways:
Suppose that we want to construct subsets $S_1, \ldots, S_m \subseteq \{1,\ldots,n\}$ with the following properties:
| $ | S_i | \geq k$ for all $i$ |
| $ | S_i \cap S_j | \leq 1$ for all $i \neq j$ |
The goal is to construct as large a family of such subsets as possible (i.e., to make $m$ as large as possible). If $k \geq 2\sqrt{n}$, then up to constants it is not hard to show that the optimal number of sets is $\frac{n}{k}$ (that is, the trivial construction with all sets disjoint is essentially the best we can do).
Here I am interested in the case when $k \ll \sqrt{n}$. In this case I claim that we can substantially outperform the trivial construction: we can take $m = \Omega(n^2 / k^3)$. The proof is a very nice application of the asymmetric Lovasz Local Lemma. (Readers can refresh their memory here on what the asymmetric LLL says.)
Read moreI’ve spent much of the last few days reading various ICML papers and I find there’s a few pieces of feedback that I give consistently across several papers. I’ve collated some of these below. As a general note, many of these are about local style rather than global structure; I think that good local style probably contributes substantially more to readability than global structure and is in general under-rated. I’m in general pretty willing to break rules about global structure (such as even having a conclusion section in the first place! though this might cause reviewers to look at your paper funny), but not to break local stylistic rules without strong reasons.
General Writing Advice
In my previous post, “Latent Variables and Model Mis-specification”, I argued that while machine learning is good at optimizing accuracy on observed signals, it has less to say about correctly inferring the values for unobserved variables in a model. In this post I’d like to focus in on a specific context for this: inverse reinforcement learning (Ng et al. 2000, Abeel et al. 2004, Ziebart et al. 2008, Ho et al 2016), where one observes the actions of an agent and wants to infer the preferences and beliefs that led to those actions. For this post, I am pleased to be joined by Owain Evans, who is an active researcher in this area and has co-authored an online book about building models of agents (see here in particular for a tutorial on inverse reinforcement learning and inverse planning).
Owain and I are particularly interested in inverse reinforcement learning (IRL) because it has been proposed (most notably by Stuart Russell) as a method for learning human values in the context of AI safety; among other things, this would eventually involve learning and correctly implementing human values by artificial agents that are much more powerful, and act with much broader scope, than any humans alive today. While we think that overall IRL is a promising route to consider, we believe that there are also a number of non-obvious pitfalls related to performing IRL with a mis-specified model. The role of IRL in AI safety is to infer human values, which are represented by a reward function or utility function. But crucially, human values (or human reward functions) are never directly observed.
Read moreHere is interesting linear algebra fact: let $A$ be an $n \times n$ matrix and $u$ be a vector such that $u^{\top}A = \lambda u^{\top}$. Then for any matrix $B$, $u^{\top}((A-B)(\lambda I - B)^{-1}) = u^{\top}$.
The proof is just basic algebra: $u^{\top}(A-B)(\lambda I - B)^{-1} = (\lambda u^{\top} - u^{\top}B)(\lambda I - B)^{-1} = u^{\top}(\lambda I - B)(\lambda I - B)^{-1} = u^{\top}$.
Why care about this? Let’s imagine that $A$ is a (not necessarily symmetric) stochastic matrix, so $1^{\top}A = 1^{\top}$. Let $A-B$ be a low-rank approximation to $A$ (so $A-B$ consists of all the large singular values, and $B$ consists of all the small singular values). Unfortunately since $A$ is not symmetric, this low-rank approximation doesn’t preserve the eigenvalues of $A$ and so we need not have $1^{\top}(A-B) = 1^{\top}$. The $(I-B)^{-1}$ can be thought of as a “correction” term such that the resulting matrix is still low-rank, but we’ve preserved one of the eigenvectors of $A$.
Read moreConsider the following statements:
What do these all have in common? Despite being fairly non-trivial and deep results, they all can be proved in less than half of a page using the Prékopa–Leindler inequality.
(I won’t show this here, or give formal versions of the statements above, but time permitting I will do so in a later blog post.)
Read moreMachine learning is very good at optimizing predictions to match an observed signal — for instance, given a dataset of input images and labels of the images (e.g. dog, cat, etc.), machine learning is very good at correctly predicting the label of a new image. However, performance can quickly break down as soon as we care about criteria other than predicting observables. There are several cases where we might care about such criteria:
In my post on where I plan to donate in 2016, I said that I would set aside \$2000 for funding promising projects that I come across in the next year:
The idea behind the project fund is … [to] give in a low-friction way on scales that are too small for organizations like Open Phil to think about. Moreover, it is likely good for me to develop a habit of evaluating projects I come across and thinking about whether they could benefit from additional money (either because they are funding constrained, or to incentivize an individual who is on the fence about carrying the project out). Finally, if this effort is successful, it is possible that other EAs will start to do this as well, which could magnify the overall impact. I think there is some danger that I will not be able to allocate the \$2000 in the next year, in which case any leftover funds will go to next year’s donor lottery.
In this post I will give some further details about this fund. My primary goal is to give others an idea of what projects I am likely to consider funding, so that anyone who thinks they might be a good fit for this can get in contact with me. (I also expect many of the best opportunities to come from people that I meet in person but don’t necessarily read this blog, so I plan to actively look for projects throughout the year as well.)
I am looking to fund or incentivize projects that meet several of the criteria below:
Read moreThe following explains where I plan to donate in 2016, with some of my thinking behind it. This year, I had \$10,000 to allocate (the sum of my giving from 2015 and 2016, which I lumped together for tax reasons; although I think this was a mistake in retrospect, both due to discount rates and because I could have donated in January and December 2016 and still received the same tax benefits).
To start with the punch line: I plan to give \$4000 to the EA donor lottery, \$2500 to GiveWell for discretionary granting, \$2000 to be held in reserve to fund promising projects, \$500 to GiveDirectly, \$500 to the Carnegie Endowment (earmarked for the Carnegie-Tsinghua Center), and \$500 to the Blue Ribbon Study Panel.
For those interested in donating to any of these: instructions for the EA donor lottery and the Blue Ribbon Study Panel are in the corresponding links above, and you can donate to both GiveWell and GiveDirectly at this page. I am looking in to whether it is possible for small donors to give to the Carnegie Endowment, and will update this page when I find out.
Read moreWhen I meet someone who works in a field outside of computer science, I usually ask them a lot of questions about their field that I’m curious about. (This is still relevant even if I’ve already met someone in that field before, because it gives me an idea of the range of expert consensus; for some questions this ends up being surprisingly variable.) I often find that, as an outsider, I can think of natural-seeming questions that experts in the field haven’t thought about, because their thinking is confined by their field’s paradigm while mine is not (pessimistically, it’s instead constrained by a different paradigm, i.e. computer science).
Usually my questions are pretty naive, and are basically what a computer scientist would think to ask based on their own biases. For instance:
Here are two strange facts about matrices, which I can prove but not in a satisfying way.
If anyone has insight into either of these, I’d be very interested!
Read moreSuppose that we have a random variable $X \in \mathbb{R}^d$, such that $\mathbb{E}[XX^{\top}] = I_{d \times d}$. Now take k independent Gaussian random variables $Z_1, \ldots, Z_k \sim \mathcal{N}(0, I_{d \times d})$, and let J be the argmax (over j in 1, …, k) of $Z_j^{\top}X$.
It seems that it should be very hard to predict J well, in the following sense: for any function $q(j \mid x)$, the expectation of $\mathbb{E}_{x}[q(J \mid x)]$, should with high probability be very close to $\frac{1}{k}$ (where the second probability is taken over the randomness in $Z$). In fact, Alex Zhai and I think that the probability of the expectation exceeding $\frac{1}{k}$ should be at most $\exp(-C(\epsilon/k)^2d)$ for some constant C. (We can already show this to be true where we replace $(\epsilon/k)^2$ with $(\epsilon/k)^4$.) I will not sketch a proof here but the idea is pretty cool, it basically uses Lipschitz concentration of Gaussian random variables.
Read moreConsider a probability distribution ${p(y)}$ on a space ${\mathcal{Y}}$. Suppose we want to construct a set ${\mathcal{P}}$ of probability distributions on ${\mathcal{Y}}$ such that ${p(y)}$ is the maximum-entropy distribution over ${\mathcal{P}}$:
$\displaystyle H(p) = \max_{q \in \mathcal{P}} H(q), $
where ${H(p) = \mathbb{E}_{p}[-\log p(y)]}$ is the entropy. We call such a set a maximum-entropy set for ${p}$. Furthermore, we would like ${\mathcal{P}}$ to be as large as possible, subject to the constraint that ${\mathcal{P}}$ is convex.
Does such a maximal convex maximum-entropy set ${\mathcal{P}}$ exist? That is, is there some convex set ${\mathcal{P}}$ such that ${p}$ is the maximum-entropy distribution in ${\mathcal{P}}$, and for any ${\mathcal{Q}}$ satisfying the same property, ${\mathcal{Q} \subseteq \mathcal{P}}$? It turns out that the answer is yes, and there is even a simple characterization of ${\mathcal{P}}$:
Read moreThere has been much recent discussion about AI risk, meaning specifically the potential pitfalls (both short-term and long-term) that AI with improved capabilities could create for society. Discussants include AI researchers such as Stuart Russell and Eric Horvitz and Tom Dietterich, entrepreneurs such as Elon Musk and Bill Gates, and research institutes such as the Machine Intelligence Research Institute (MIRI) and Future of Humanity Institute (FHI); the director of the latter institute, Nick Bostrom, has even written a bestselling book on this topic. Finally, ten million dollars in funding have been earmarked towards research on ensuring that AI will be safe and beneficial. Given this, I think it would be useful for AI researchers to discuss the nature and extent of risks that might be posed by increasingly capable AI systems, both short-term and long-term. As a PhD student in machine learning and artificial intelligence, this essay will describe my own views on AI risk, in the hopes of encouraging other researchers to detail their thoughts, as well.
Read more[Highlights for the busy: de-bunking standard “Bayes is optimal” arguments; frequentist Solomonoff induction; and a description of the online learning framework.]
Short summary. This essay makes many points, each of which I think is worth reading, but if you are only going to understand one point I think it should be “Myth 5″ below, which describes the online learning framework as a response to the claim that frequentist methods need to make strong modeling assumptions. Among other things, online learning allows me to perform the following remarkable feat: if I’m betting on horses, and I get to place bets after watching other people bet but before seeing which horse wins the race, then I can guarantee that after a relatively small number of races, I will do almost as well overall as the best other person, even if the number of other people is very large (say, 1 billion), and their performance is correlated in complicated ways.
If you’re only going to understand two points, then also read about the frequentist version of Solomonoff induction, which is described in “Myth 6″.
Main article. I’ve already written one essay on Bayesian vs. frequentist statistics. In that essay, I argued for a balanced, pragmatic approach in which we think of the two families of methods as a collection of tools to be used as appropriate. Since I’m currently feeling contrarian, this essay will be far less balanced and will argue explicitly against Bayesian methods and in favor of frequentist methods. I hope this will be forgiven as so much other writing goes in the opposite direction of unabashedly defending Bayes. I should note that this essay is partially inspired by some of Cosma Shalizi’s blog posts, such as this one.
Read moreI’ve decided to branch out a bit from technical discussions and engage in, as Scott Aaronson would call it, some metaphysical spouting. The topic of today is the effective altruism movement. I’m about to be relentlessly critical of it, so this is probably not the best post to read as your first introduction. Instead, read this and this. Then you can read what follows (but keep in mind that there are also many good things about the EA movement that I’m failing to mention here).
Read moreAn important concept in online learning and convex optimization is that of strong convexity: a twice-differentiable function $f$ is said to be strongly convex with respect to a norm $\|\cdot\|$ if
$z^T\frac{\partial^2 f}{\partial x^2}z \geq \|z\|^2$
for all $z$ (for functions that are not twice-differentiable, there is an analogous criterion in terms of the Bregman divergence). To check strong convexity, then, we basically need to check a condition on the Hessian, namely that $z^THz \geq \|z\|^2$. So, under what conditions does this hold?
For the $l^2$ norm, the answer is easy: $z^THz \geq \|z\|_2^2$ if and only if $H \succeq I$ (i.e., $H-I$ is positive semidefinite). This can be shown in many ways, perhaps the easiest is by noting that $z^THz-\|z\|_2^2 = z^T(H-I)z$.
For the $l^{\infty}$ norm, the answer is a bit trickier but still not too complicated. Recall that we want necessary and sufficient conditions under which $z^THz \geq \|z\|_{\infty}^2$. Note that this is equivalent to asking that $z^THz \geq (z_i)^2$ for each coordinate $i$ of $z$, which in turn is equivalent to $H \succeq e_ie_i^T$ for each coordinate vector $e_i$ (these are the vectors that are 1 in the $i$th coordinate and 0 everywhere else).
Read moreHere’s a fun counterexample: a function $\mathbb{R}^n \to \mathbb{R}$ that is jointly convex in any $n-1$ of the variables, but not in all variables at once. The function is
$f(x_1,\ldots,x_n) = \frac{1}{2}(n-1.5)\sum_{i=1}^n x_i^2 - \sum_{i < j} x_ix_j$
To see why this is, note that the Hessian of $f$ is equal to
$\left[ \begin{array}{cccc} n-1.5 & -1 & \cdots & -1 \\ -1 & n-1.5 & \cdots & -1 \\ \vdots & \vdots & \ddots & \vdots \\ -1 & -1 & \cdots & n-1.5 \end{array} \right]$
This matrix is equal to $(n-0.5)I - J$, where $I$ is the identity matrix and $J$ is the all-ones matrix, which is rank 1 and whose single non-zero eigenvalue is $n$. Therefore, this matrix has $n-1$ eigenvalues of $n-0.5$, as well as a single eigenvalue of $-0.5$, and hence is not positive definite.
On the other hand, any submatrix of size $n-1$ is of the form $(n-0.5)I-J$, but where now $J$ is only $(n-1) \times (n-1)$. This matrix now has $n-2$ eigenvalues of $n-0.5$, together with a single eigenvalue of $0.5$, and hence is positive definite. Therefore, the Hessian is positive definite when restricted to any $n-1$ variables, and hence $f$ is convex in any $n-1$ variables, but not in all $n$ variables jointly.
Read more(This post represents research in progress. I may think about these concepts entirely differently a few months from now, but for my own benefit I’m trying to exposit on them in order to force myself to understand them better.)
For many inference tasks, especially ones with either non-linearities or non-convexities, it is common to use particle-based methods such as beam search, particle filters, sequential Monte Carlo, or Markov Chain Monte Carlo. In these methods, we approximate a distribution by a collection of samples from that distribution, then update the samples as new information is added. For instance, in beam search, if we are trying to build up a tree, we might build up a collection of $K$ samples for the left and right subtrees, then look at all $K^2$ ways of combining them into the entire tree, but then downsample again to the $K$ trees with the highest scores. This allows us to search through the exponentially large space of all trees efficiently (albeit at the cost of possibly missing high-scoring trees).
One major problem with such particle-based methods is diversity: the particles will tend to cluster around the highest-scoring mode, rather than exploring multiple local optima if they exist. This can be bad because it makes learning algorithms overly myopic. Another problem, especially in combinatorial domains, is difficulty of partial evaluation: if we have some training data that we are trying to fit to, and we have chosen settings of some, but not all, variables in our model, it can be difficult to know if that setting is on the right track (for instance, it can be difficult to know whether a partially-built tree is a promising candidate or not). For time-series modeling, this isn’t nearly as large of a problem, since we can evaluate against a prefix of the time series to get a good idea (this perhaps explains the success of particle filters in these domains).
Read moreFor collections of independent random variables, the Chernoff bound and related bounds give us very sharp concentration inequalities — if $X_1,\ldots,X_n$ are independent, then their sum has a distribution that decays like $e^{-x^2}$. For random variables that are only pairwise independent, the strongest bound we have is Chebyshev’s inequality, which says that their sum decays like $\frac{1}{x^2}$.
The point of this post is to construct an equality case for Chebyshev: a collection of pairwise independent random variables whose sum does not satisfy the concentration bound of Chernoff, and instead decays like $\frac{1}{x^2}$.
Read moreI spent the last several hours trying to come up with an efficient algorithm to the following problem:
Problem: Suppose that we have a sequence of $l$ pairs of non-negative numbers $(a_1,b_1),\ldots,(a_l,b_l)$ such that $\sum_{i=1}^l a_i \leq A$ and $\sum_{i=1}^l b_i \leq B$. Devise an efficient algorithm to find the $k$ pairs $(a_{i_1},b_{i_1}),\ldots,(a_{i_k},b_{i_k})$ that maximize
$\left[\sum_{r=1}^k a_{i_r}\log(a_{i_r}/b_{i_r})\right] + \left[A-\sum_{r=1}^k a_{i_r}\right]\log\left(\frac{A-\sum_{r=1}^k a_{i_r}}{B-\sum_{r=1}^k b_{i_r}}\right).$
Read moreWhile grading homeworks today, I came across the following bound:
Theorem 1: If A and B are symmetric $n\times n$ matrices with eigenvalues $\lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_n$ and $\mu_1 \geq \mu_2 \geq \ldots \geq \mu_n$ respectively, then $Trace(A^TB) \leq \sum_{i=1}^n \lambda_i \mu_i$.
For such a natural-looking statement, this was surprisingly hard to prove. However, I finally came up with a proof, and it was cool enough that I felt the need to share. To prove this, we actually need two ingredients. The first is the Cauchy Interlacing Theorem:
Theorem 2: If A is an $n\times n$ symmetric matrix and B is an $(n-k) \times (n-k)$ principle submatrix of A, then $\lambda_{i-k}(A) \leq \lambda_i(B) \leq \lambda_i(A)$, where $\lambda_i(X)$ is the ith largest eigenvalue of X.
Read moreThe KL divergence is an important tool for studying the distance between two probability distributions. Formally, given two distributions $p$ and $q$, the KL divergence is defined as
| $KL(p | q) := \int p(x) \log(p(x)/q(x)) dx$ |
| Note that $KL(p | q) \neq KL(q | p)$. Intuitively, a small $KL(p | q)$ means that there are few points that $p$ assigns high probability to but that $q$ does not. We can also think of $KL(p | q)$ as the number of bits of information needed to update from the distribution $q$ to the distribution $p$. |
| Suppose that p and q are both mixtures of other distributions: $p(x) = \sum_i \alpha_i F_i(x)$ and $q(x) = \sum_i \beta_i G_i(x)$. Can we bound $KL(p | q)$ in terms of the $KL(F_i | G_i)$? In some sense this is asking to upper bound the KL divergence in terms of some more local KL divergence. It turns out this can be done: |
Theorem: If $\sum_i \alpha_i = \sum_i \beta_i = 1$ and $F_i$ and $G_i$ are all probability distributions, then
| $KL\left(\sum_i \alpha_i F_i | \sum_i \beta_i G_i\right) \leq \sum_i \alpha_i \left(\log(\alpha_i/\beta_i) + KL(F_i | G_i)\right)$. |
Today Arun asked me the following question:
“Under what conditions will a set $\{p_1,\ldots,p_n\}$ of polynomials be quadratically independent, in the sense that $\{p_1^2, p_1p_2, p_2^2, p_1p_3,\ldots,p_{n-1}p_n, p_n^2\}$ is a linearly independent set?”
I wasn’t able to make much progress on this general question, but in the specific setting where the $p_i$ are all polynomials in one variable, and we further restrict to just monomials, (i.e. $p_i(x) = x^{d_i}$ for some $d_i$), the condition is just that there are no distinct unordered pairs $(i_1,j_1),(i_2,j_2)$ such that $d_{i_1} + d_{j_1} = d_{i_2} + d_{j_2}$. Arun was interested in the largest such a set could be for a given maximum degree $D$, so we are left with the following interesting combinatorics problem:
“What is the largest subset $S$ of $\{1,\ldots,D\}$ such that no two distinct pairs of elements of $S$ have the same sum?”
For convenience of notation let $n$ denote the size of $S$. A simple upper bound is $\binom{N+1}{2} \leq 2D-1$, since there are $\binom{N+1}{2}$ pairs to take a sum of, and all pairwise sums lie between $2$ and $2D$. We therefore have $n = O(\sqrt{D})$.
Read moreIn my last post I discussed log-linear models. In this post I’d like to take another perspective on log-linear models, by thinking of them as members of an exponential family. There are many reasons to take this perspective: exponential families give us efficient representations of log-linear models, which is important for continuous domains; they always have conjugate priors, which provide an analytically tractable regularization method; finally, they can be viewed as maximum-entropy models for a given set of sufficient statistics. Don’t worry if these terms are unfamiliar; I will explain all of them by the end of this post. Also note that most of this material is available on the Wikipedia page on exponential families, which I used quite liberally in preparing the below exposition.
An exponential family is a family of probability distributions, parameterized by ${\theta \in \mathbb{R}^n}$, of the form
$p(x \mid \theta) \propto h(x)\exp(\theta^T\phi(x)).$ (1)
Read moreI’ve decided to start recording algebra tricks as I end up using them. Today I actually have two tricks, but they end up being used together a lot. I don’t know if they have more formal names, but I call them the “trace trick” and the “rank 1 relaxation”.
Suppose that we want to maximize the Rayleigh quotient $\frac{x^TAx}{x^Tx}$ of a matrix $A$. There are many reasons we might want to do this, for instance of $A$ is symmetric then the maximum corresponds to the largest eigenvalue. There are also many ways to do this, and the one that I’m about to describe is definitely not the most efficient, but it has the advantage of being flexible, in that it easily generalizes to constrained maximizations, etc.
The first observation is that $\frac{x^TAx}{x^Tx}$ is homogeneous, meaning that scaling $x$ doesn’t affect the result. So, we can assume without loss of generality that $x^Tx = 1$, and we end up with the optimization problem:
maximize $x^TAx$
subject to $x^Tx = 1$
This is where the trace trick comes in. Recall that the trace of a matrix is the sum of its diagonal entries. We are going to use two facts: first, the trace of a number is just the number itself. Second, trace(AB) = trace(BA). (Note, however, that trace(ABC) is not in general equal to trace(BAC), although trace(ABC) is equal to trace(CAB).) We use these two properties as follows — first, we re-write the optimization problem as:
Read moreI’ve spent most of my research career trying to build big, complex nonparametric models; however, I’ve more recently delved into the realm of natural language processing, where how awesome your model looks on paper is irrelevant compared to how well it models your data. In the spirit of this new work (and to lay the groundwork for a later post on NLP), I’d like to go over a family of models that I think is often overlooked due to not being terribly sexy (or at least, I overlooked it for a good while). This family is the family of log-linear models, which are models of the form:
$p(x \mid \theta) \propto e^{\phi(x)^T\theta}, $
where ${\phi}$ maps a data point to a feature vector; they are called log-linear because the log of the probability is a linear function of ${\phi(x)}$. We refer to ${\phi(x)^T\theta}$ as the score of ${x}$.
This model class might look fairly restricted at first, but the real magic comes in with the feature vector ${\phi}$. In fact, every probabilistic model that is absolutely continuous with respect to Lebesgue measure can be represented as a log-linear model for sufficient choices of ${\phi}$ and $\theta$. This is actually trivially true, as we can just take ${\phi : X \rightarrow \mathbb{R}}$ to be ${\log p(x)}$ and $\theta$ to be ${1}$.
Read more(This is available in pdf form here.)
If you are a newly initiated student into the field of machine learning, it won’t be long before you start hearing the words “Bayesian” and “frequentist” thrown around. Many people around you probably have strong opinions on which is the “right” way to do statistics, and within a year you’ve probably developed your own strong opinions (which are suspiciously similar to those of the people around you, despite there being a much greater variance of opinion between different labs). In fact, now that the year is 2012 the majority of new graduate students are being raised as Bayesians (at least in the U.S.) with frequentists thought of as stodgy emeritus professors stuck in their ways.
If you are like me, the preceding set of facts will make you very uneasy. They will make you uneasy because simple pattern-matching – the strength of people’s opinions, the reliability with which these opinions split along age boundaries and lab boundaries, and the ridicule that each side levels at the other camp – makes the “Bayesians vs. frequentists” debate look far more like politics than like scholarly discourse. Of course, that alone does not necessarily prove anything; these disconcerting similarities could just be coincidences that I happened to cherry-pick.
Read moreI just finished presenting my recent paper on stochastic verification at RSS 2011. There is a conference version online, with a journal article to come later. In this post I want to go over the problem statement and my solution.
Problem Statement
Abstractly, the goal is to be given some sort of description of a system, and of a goal for that system, and then verify that the system will reach that goal. The difference between our work and a lot (but not all) of the previous work is that we want to work with an explicit noise model for the system. So, for instance, I tell you that the system satisfies
$dx(t) = f(x) dt + g(x) dw(t),$
where $f(x)$ represents the nominal dynamics of the system, $g(x)$ represents how noise enters the system, and $dw(t)$ is a standard Wiener process (the continuous-time version of Gaussian noise). I would like to, for instance, verify that $h(x(T)) < 0$ for some function $h$ and some final time $T$. For example, if $x$ is one-dimensional then I could ask that $x(10)^2-1 < 0$, which is asking for $x$ to be within a distance of $1$ of the origin at time $10$. For now, I will focus on time-invariant systems and stability conditions. This means that $f$ and $g$ are not functions of $t$, and the condition we want to verify is that $h(x(t)) < 0$ for all $t \in [0,T]$. However, it is not too difficult to extend these ideas to the time-varying case, as I will show in the results at the end.
Read moreI have spent the last several months doing applied math, culminating in a submission of a paper to a robotics conference (although culminating might be the wrong word, since I’m still working on the project).
Unfortunately the review process is double-blind so I can’t talk about that specifically, but I’m more interested in going over the math I ended up using (not expositing on it, just making a list, more or less). This is meant to be a moderate amount of empirical evidence for which pieces of math are actually useful, and which aren’t (of course, the lack of appearance on this list doesn’t imply uselessness, but should be taken as Bayesian evidence against usefulness).
I’ll start with the stuff that I actually used in the paper, then stuff that helped me formulate the ideas in the paper, then stuff that I’ve used in other work that hasn’t yet come to fruition. These will be labelled I, II, and III below. Let me know if you think something should be in III that isn’t [in other words, you think there’s a piece of math that is useful but not listed here, preferably with the application you have in mind], or if you have better links to any of the topics below.
Read moreHumans are very good at correctly generalizing rules across categories (at least, compared to computers). In this post I will examine mechanisms that would allow us to do this in a reasonably rigorous manner. To this end I will present a probabilistic model such that conditional inference on that model leads to generalization across a category.
There are three questions along these lines that I hope to answer:
I suspect that the mechanisms for each of these is rather complex, but I am reasonably confident that the methods I present make up at least part of the actual answer. A good exercise is to come up with examples where these methods fail.
Read moreWhat happens when you are uncertain about observations you made? For instance, you remember something happening, but you don’t remember who did it. Or you remember some fact you read on wikipedia, but you don’t know whether it said that hydrogen or helium was used in some chemical process.
How do we take this information into account in the context of Bayes’ rule? First, I’d like to note that there are different ways something could be uncertain. It could be that you observed X, but you don’t remember if it was in state A or state B. Or it could be that you think you observed X in state A, but you aren’t sure.
These are different because in the first case you don’t know whether to concentrate probability mass towards A or B, whereas in the second case you don’t know whether to concentrate probability mass at all.
Fortunately, both cases are pretty straightforward as long as you are careful about using Bayes’ rule. However, today I am going to focus on the latter case. In fact, I will restrict my attention to the following problem:
Read moreYou have a coin that has some probability $\pi$ of coming up heads. You also know that all flips of this coin are independent. But you don’t know what $\pi$ is. However, you have observed this coin $n$ times in the past. But for each observation, you aren’t completely sure that this was the coin you were observing. In particular, you only assign a probability $r_i$ to your $i$th observation actually being about this coin. Given this, and the sequence of heads and tails you remember, what is your estimate of $\pi?$
The goal of this post is to give an overview of Bayesian statistics as well as to correct errors about probability that even mathematically sophisticated people commonly make. Hopefully by the end of this post I will convince you that you don’t actually understand probability theory as well as you think, and that probability itself is something worth thinking about.
I will try to make this post somewhat shorter than the previous posts. As a result, this will be only the first of several posts on probability. Even though this post will be shorter, I will summarize its organization below:
I ended my last post on a somewhat dire note, claiming that least squares can do pretty terribly when fitting data. It turns out that things aren’t quite as bad as I thought, but most likely worse than you would expect.
The theme of this post is going to be things you use all the time (or at least, would use all the time if you were an electrical engineer), but probably haven’t ever thought deeply about. I’m going to include a combination of mathematical proofs and matlab demonstrations, so there should hopefully be something here for everyone.
My first topic is going to be, as promised, least squares curve fitting. I’ll start by talking about situations when it can fail, and also about situations when it is “optimal” in some well-defined sense. To do that, I’ll have to use some Fourier analysis, which will present a good opportunity to go over when frequency-domain methods can be very useful, when they can fail, and what you can try to do when they fail.
To start, I’m going to do a simple matlab experiment. I encourage you to follow along if you have matlab (if you have MIT certificates you can get it for free at http://matlab.mit.edu/).
Read moreLast time I talked about linear control, I presented a Linear Quadratic Regulator as a general purpose hammer for solving linear control problems. In this post I’m going to explain why LQR by itself is not enough (even for nominally linear systems). (Author’s note: I got to the end of the post and realized I didn’t fulfill my promise in the previous sentence. So it’s redacted, but will hopefully be dealt with in a later post.) Then I’m going to do my best to introduce a lot of the standard ideas in linear control theory.
My motivation for this is that, even though these ideas have a reasonably nice theory from a mathematical standpoint, they are generally presented from an engineering standpoint. And although all of the math is right there, and I’m sure that professional control theorists understand it much better than I do, I found that I had to go to a lot of effort to synthesize a good mathematical explanation of the underlying theory.
However, this effort was not due to any inherent difficulties in the theory itself, but rather, like I said, a disconnect in the intuition of, and issues relevant to, an engineer versus a mathematician. I’m not going to claim that one way of thinking is better than the other, but my way of thinking, and I assume that of most of my audience, falls more in line with the mathematical viewpoint. What’s even better is that many of the techniques built up for control theory have interesting ramifications when considered as statements about vector spaces. I hope that you’ll find the exposition illuminating.
Read moreMy last few posts have been rather abstract. I thought I’d use this one to go into some details about the actual system we’re working with.
As I mentioned before, we are looking at a cart pole in a water tunnel. A cart pole is sometimes also called an inverted pendulum. Here is a diagram from wikipedia:
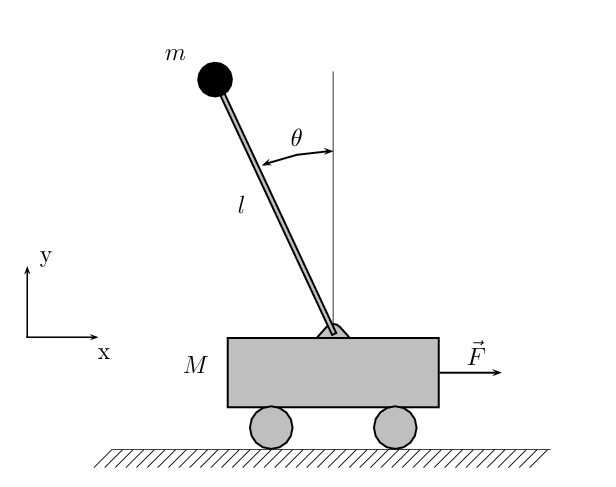
The parameter we have control over is F, the force on the cart. We would like to use this to control both the position of the cart and the angle of the pendulum. If the cart is standing still, the only two possible fixed points of the system are $\theta = 0$ (the bottom, or “downright”) and $\theta = \pi$ (the “upright”). Since $\theta = 0$ is easy to get to, we will be primarily interested with getting to $\theta = \pi$.
Read moreThe purpose of this post is to introduce you to some of the basics of control theory and to introduce the Linear-Quadratic Regulator, an extremely good hammer for solving stabilization problems.
To start with, what do we mean by a control problem? We mean that we have some system with dynamics described by an equation of the form
$\dot{x} = Ax,$
where $x$ is the state of the system and $A$ is some matrix (which itself is allowed to depend on $x$). For example, we could have an object that is constrained to move in a line along a frictionless surface. In this case, the system dynamics would be
$\left[ \begin{array}{c} \dot{q} \\ \ddot{q} \end{array} \right] = \left[ \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array} \right]\left[ \begin{array}{c} q \\ \dot{q} \end{array} \right]. $
Read moreThis summer I am working in the Robotics Locomotion group at CSAIL (MIT’s Computer Science and Artificial Intelligence Laboratory). I’ve decided to start a blog to exposit on the ideas involved. This ranges from big theoretical ideas (like general system identification techniques) to problem-specific ideas (specific learning strategies for the system we’re interested in) to useful information on using computational tools (how to make MATLAB’s ode45 do what you want it to).
To start with, I’m going to describe the problem that I’m working on, together with John (a grad student in mechanical engineering).
Last spring, I took 6.832 (Underactuated Robotics) at MIT. In that class, we learned multiple incredibly powerful techniques for nonlinear control. After taking it, I was more or less convinced that we could solve, at least off-line, pretty much any control problem once it was posed properly. After coming to the Locomotion group, I realized that this wasn’t quite right. What is actually true is that we can solve any control problem where we have a good model and a reasonable objective function (we can also run into problems in high dimensions, but even there you can make progress if the objective function is nice enough).
Read moreThis summer I am working in the Robotics Locomotion group at CSAIL (MIT’s Computer Science and Artificial Intelligence Laboratory). I’ve decided to start a blog to exposit on the ideas involved. This ranges from big theoretical ideas (like general system identification techniques) to problem-specific ideas (specific learning strategies for the system we’re interested in) to useful information on using computational tools (how to make MATLAB’s ode45 do what you want it to).
To start with, I’m going to describe the problem that I’m working on, together with John (a grad student in mechanical engineering).
Last spring, I took 6.832 (Underactuated Robotics) at MIT. In that class, we learned multiple incredibly powerful techniques for nonlinear control. After taking it, I was more or less convinced that we could solve, at least off-line, pretty much any control problem once it was posed properly. After coming to the Locomotion group, I realized that this wasn’t quite right. What is actually true is that we can solve any control problem where we have a good model and a reasonable objective function (we can also run into problems in high dimensions, but even there you can make progress if the objective function is nice enough).
Read moreThe purpose of this post is to introduce you to some of the basics of control theory and to introduce the Linear-Quadratic Regulator, an extremely good hammer for solving stabilization problems.
To start with, what do we mean by a control problem? We mean that we have some system with dynamics described by an equation of the form
$\dot{x} = Ax,$
where $x$ is the state of the system and $A$ is some matrix (which itself is allowed to depend on $x$). For example, we could have an object that is constrained to move in a line along a frictionless surface. In this case, the system dynamics would be
$\left[ \begin{array}{c} \dot{q} \\ \ddot{q} \end{array} \right] = \left[ \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array} \right]\left[ \begin{array}{c} q \\ \dot{q} \end{array} \right]. $
Read moreMy last few posts have been rather abstract. I thought I’d use this one to go into some details about the actual system we’re working with.
As I mentioned before, we are looking at a cart pole in a water tunnel. A cart pole is sometimes also called an inverted pendulum. Here is a diagram from wikipedia:

The parameter we have control over is F, the force on the cart. We would like to use this to control both the position of the cart and the angle of the pendulum. If the cart is standing still, the only two possible fixed points of the system are $\theta = 0$ (the bottom, or “downright”) and $\theta = \pi$ (the “upright”). Since $\theta = 0$ is easy to get to, we will be primarily interested with getting to $\theta = \pi$.
Read moreLast time I talked about linear control, I presented a Linear Quadratic Regulator as a general purpose hammer for solving linear control problems. In this post I’m going to explain why LQR by itself is not enough (even for nominally linear systems). (Author’s note: I got to the end of the post and realized I didn’t fulfill my promise in the previous sentence. So it’s redacted, but will hopefully be dealt with in a later post.) Then I’m going to do my best to introduce a lot of the standard ideas in linear control theory.
My motivation for this is that, even though these ideas have a reasonably nice theory from a mathematical standpoint, they are generally presented from an engineering standpoint. And although all of the math is right there, and I’m sure that professional control theorists understand it much better than I do, I found that I had to go to a lot of effort to synthesize a good mathematical explanation of the underlying theory.
However, this effort was not due to any inherent difficulties in the theory itself, but rather, like I said, a disconnect in the intuition of, and issues relevant to, an engineer versus a mathematician. I’m not going to claim that one way of thinking is better than the other, but my way of thinking, and I assume that of most of my audience, falls more in line with the mathematical viewpoint. What’s even better is that many of the techniques built up for control theory have interesting ramifications when considered as statements about vector spaces. I hope that you’ll find the exposition illuminating.
Read moreI ended my last post on a somewhat dire note, claiming that least squares can do pretty terribly when fitting data. It turns out that things aren’t quite as bad as I thought, but most likely worse than you would expect.
The theme of this post is going to be things you use all the time (or at least, would use all the time if you were an electrical engineer), but probably haven’t ever thought deeply about. I’m going to include a combination of mathematical proofs and matlab demonstrations, so there should hopefully be something here for everyone.
My first topic is going to be, as promised, least squares curve fitting. I’ll start by talking about situations when it can fail, and also about situations when it is “optimal” in some well-defined sense. To do that, I’ll have to use some Fourier analysis, which will present a good opportunity to go over when frequency-domain methods can be very useful, when they can fail, and what you can try to do when they fail.
To start, I’m going to do a simple matlab experiment. I encourage you to follow along if you have matlab (if you have MIT certificates you can get it for free at http://matlab.mit.edu/).
Read moreThe goal of this post is to give an overview of Bayesian statistics as well as to correct errors about probability that even mathematically sophisticated people commonly make. Hopefully by the end of this post I will convince you that you don’t actually understand probability theory as well as you think, and that probability itself is something worth thinking about.
I will try to make this post somewhat shorter than the previous posts. As a result, this will be only the first of several posts on probability. Even though this post will be shorter, I will summarize its organization below:
What happens when you are uncertain about observations you made? For instance, you remember something happening, but you don’t remember who did it. Or you remember some fact you read on wikipedia, but you don’t know whether it said that hydrogen or helium was used in some chemical process.
How do we take this information into account in the context of Bayes’ rule? First, I’d like to note that there are different ways something could be uncertain. It could be that you observed X, but you don’t remember if it was in state A or state B. Or it could be that you think you observed X in state A, but you aren’t sure.
These are different because in the first case you don’t know whether to concentrate probability mass towards A or B, whereas in the second case you don’t know whether to concentrate probability mass at all.
Fortunately, both cases are pretty straightforward as long as you are careful about using Bayes’ rule. However, today I am going to focus on the latter case. In fact, I will restrict my attention to the following problem:
Read moreYou have a coin that has some probability $\pi$ of coming up heads. You also know that all flips of this coin are independent. But you don’t know what $\pi$ is. However, you have observed this coin $n$ times in the past. But for each observation, you aren’t completely sure that this was the coin you were observing. In particular, you only assign a probability $r_i$ to your $i$th observation actually being about this coin. Given this, and the sequence of heads and tails you remember, what is your estimate of $\pi?$
Humans are very good at correctly generalizing rules across categories (at least, compared to computers). In this post I will examine mechanisms that would allow us to do this in a reasonably rigorous manner. To this end I will present a probabilistic model such that conditional inference on that model leads to generalization across a category.
There are three questions along these lines that I hope to answer:
I suspect that the mechanisms for each of these is rather complex, but I am reasonably confident that the methods I present make up at least part of the actual answer. A good exercise is to come up with examples where these methods fail.
Read moreI have spent the last several months doing applied math, culminating in a submission of a paper to a robotics conference (although culminating might be the wrong word, since I’m still working on the project).
Unfortunately the review process is double-blind so I can’t talk about that specifically, but I’m more interested in going over the math I ended up using (not expositing on it, just making a list, more or less). This is meant to be a moderate amount of empirical evidence for which pieces of math are actually useful, and which aren’t (of course, the lack of appearance on this list doesn’t imply uselessness, but should be taken as Bayesian evidence against usefulness).
I’ll start with the stuff that I actually used in the paper, then stuff that helped me formulate the ideas in the paper, then stuff that I’ve used in other work that hasn’t yet come to fruition. These will be labelled I, II, and III below. Let me know if you think something should be in III that isn’t [in other words, you think there’s a piece of math that is useful but not listed here, preferably with the application you have in mind], or if you have better links to any of the topics below.
Read moreI just finished presenting my recent paper on stochastic verification at RSS 2011. There is a conference version online, with a journal article to come later. In this post I want to go over the problem statement and my solution.
Problem Statement
Abstractly, the goal is to be given some sort of description of a system, and of a goal for that system, and then verify that the system will reach that goal. The difference between our work and a lot (but not all) of the previous work is that we want to work with an explicit noise model for the system. So, for instance, I tell you that the system satisfies
$dx(t) = f(x) dt + g(x) dw(t),$
where $f(x)$ represents the nominal dynamics of the system, $g(x)$ represents how noise enters the system, and $dw(t)$ is a standard Wiener process (the continuous-time version of Gaussian noise). I would like to, for instance, verify that $h(x(T)) < 0$ for some function $h$ and some final time $T$. For example, if $x$ is one-dimensional then I could ask that $x(10)^2-1 < 0$, which is asking for $x$ to be within a distance of $1$ of the origin at time $10$. For now, I will focus on time-invariant systems and stability conditions. This means that $f$ and $g$ are not functions of $t$, and the condition we want to verify is that $h(x(t)) < 0$ for all $t \in [0,T]$. However, it is not too difficult to extend these ideas to the time-varying case, as I will show in the results at the end.
Read more(This is available in pdf form here.)
If you are a newly initiated student into the field of machine learning, it won’t be long before you start hearing the words “Bayesian” and “frequentist” thrown around. Many people around you probably have strong opinions on which is the “right” way to do statistics, and within a year you’ve probably developed your own strong opinions (which are suspiciously similar to those of the people around you, despite there being a much greater variance of opinion between different labs). In fact, now that the year is 2012 the majority of new graduate students are being raised as Bayesians (at least in the U.S.) with frequentists thought of as stodgy emeritus professors stuck in their ways.
If you are like me, the preceding set of facts will make you very uneasy. They will make you uneasy because simple pattern-matching – the strength of people’s opinions, the reliability with which these opinions split along age boundaries and lab boundaries, and the ridicule that each side levels at the other camp – makes the “Bayesians vs. frequentists” debate look far more like politics than like scholarly discourse. Of course, that alone does not necessarily prove anything; these disconcerting similarities could just be coincidences that I happened to cherry-pick.
Read moreI’ve spent most of my research career trying to build big, complex nonparametric models; however, I’ve more recently delved into the realm of natural language processing, where how awesome your model looks on paper is irrelevant compared to how well it models your data. In the spirit of this new work (and to lay the groundwork for a later post on NLP), I’d like to go over a family of models that I think is often overlooked due to not being terribly sexy (or at least, I overlooked it for a good while). This family is the family of log-linear models, which are models of the form:
$p(x \mid \theta) \propto e^{\phi(x)^T\theta}, $
where ${\phi}$ maps a data point to a feature vector; they are called log-linear because the log of the probability is a linear function of ${\phi(x)}$. We refer to ${\phi(x)^T\theta}$ as the score of ${x}$.
This model class might look fairly restricted at first, but the real magic comes in with the feature vector ${\phi}$. In fact, every probabilistic model that is absolutely continuous with respect to Lebesgue measure can be represented as a log-linear model for sufficient choices of ${\phi}$ and $\theta$. This is actually trivially true, as we can just take ${\phi : X \rightarrow \mathbb{R}}$ to be ${\log p(x)}$ and $\theta$ to be ${1}$.
Read moreI’ve decided to start recording algebra tricks as I end up using them. Today I actually have two tricks, but they end up being used together a lot. I don’t know if they have more formal names, but I call them the “trace trick” and the “rank 1 relaxation”.
Suppose that we want to maximize the Rayleigh quotient $\frac{x^TAx}{x^Tx}$ of a matrix $A$. There are many reasons we might want to do this, for instance of $A$ is symmetric then the maximum corresponds to the largest eigenvalue. There are also many ways to do this, and the one that I’m about to describe is definitely not the most efficient, but it has the advantage of being flexible, in that it easily generalizes to constrained maximizations, etc.
The first observation is that $\frac{x^TAx}{x^Tx}$ is homogeneous, meaning that scaling $x$ doesn’t affect the result. So, we can assume without loss of generality that $x^Tx = 1$, and we end up with the optimization problem:
maximize $x^TAx$
subject to $x^Tx = 1$
This is where the trace trick comes in. Recall that the trace of a matrix is the sum of its diagonal entries. We are going to use two facts: first, the trace of a number is just the number itself. Second, trace(AB) = trace(BA). (Note, however, that trace(ABC) is not in general equal to trace(BAC), although trace(ABC) is equal to trace(CAB).) We use these two properties as follows — first, we re-write the optimization problem as:
Read moreIn my last post I discussed log-linear models. In this post I’d like to take another perspective on log-linear models, by thinking of them as members of an exponential family. There are many reasons to take this perspective: exponential families give us efficient representations of log-linear models, which is important for continuous domains; they always have conjugate priors, which provide an analytically tractable regularization method; finally, they can be viewed as maximum-entropy models for a given set of sufficient statistics. Don’t worry if these terms are unfamiliar; I will explain all of them by the end of this post. Also note that most of this material is available on the Wikipedia page on exponential families, which I used quite liberally in preparing the below exposition.
An exponential family is a family of probability distributions, parameterized by ${\theta \in \mathbb{R}^n}$, of the form
$p(x \mid \theta) \propto h(x)\exp(\theta^T\phi(x)).$ (1)
Read moreToday Arun asked me the following question:
“Under what conditions will a set $\{p_1,\ldots,p_n\}$ of polynomials be quadratically independent, in the sense that $\{p_1^2, p_1p_2, p_2^2, p_1p_3,\ldots,p_{n-1}p_n, p_n^2\}$ is a linearly independent set?”
I wasn’t able to make much progress on this general question, but in the specific setting where the $p_i$ are all polynomials in one variable, and we further restrict to just monomials, (i.e. $p_i(x) = x^{d_i}$ for some $d_i$), the condition is just that there are no distinct unordered pairs $(i_1,j_1),(i_2,j_2)$ such that $d_{i_1} + d_{j_1} = d_{i_2} + d_{j_2}$. Arun was interested in the largest such a set could be for a given maximum degree $D$, so we are left with the following interesting combinatorics problem:
“What is the largest subset $S$ of $\{1,\ldots,D\}$ such that no two distinct pairs of elements of $S$ have the same sum?”
For convenience of notation let $n$ denote the size of $S$. A simple upper bound is $\binom{N+1}{2} \leq 2D-1$, since there are $\binom{N+1}{2}$ pairs to take a sum of, and all pairwise sums lie between $2$ and $2D$. We therefore have $n = O(\sqrt{D})$.
Read moreThe KL divergence is an important tool for studying the distance between two probability distributions. Formally, given two distributions $p$ and $q$, the KL divergence is defined as
| $KL(p | q) := \int p(x) \log(p(x)/q(x)) dx$ |
| Note that $KL(p | q) \neq KL(q | p)$. Intuitively, a small $KL(p | q)$ means that there are few points that $p$ assigns high probability to but that $q$ does not. We can also think of $KL(p | q)$ as the number of bits of information needed to update from the distribution $q$ to the distribution $p$. |
| Suppose that p and q are both mixtures of other distributions: $p(x) = \sum_i \alpha_i F_i(x)$ and $q(x) = \sum_i \beta_i G_i(x)$. Can we bound $KL(p | q)$ in terms of the $KL(F_i | G_i)$? In some sense this is asking to upper bound the KL divergence in terms of some more local KL divergence. It turns out this can be done: |
Theorem: If $\sum_i \alpha_i = \sum_i \beta_i = 1$ and $F_i$ and $G_i$ are all probability distributions, then
| $KL\left(\sum_i \alpha_i F_i | \sum_i \beta_i G_i\right) \leq \sum_i \alpha_i \left(\log(\alpha_i/\beta_i) + KL(F_i | G_i)\right)$. |
While grading homeworks today, I came across the following bound:
Theorem 1: If A and B are symmetric $n\times n$ matrices with eigenvalues $\lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_n$ and $\mu_1 \geq \mu_2 \geq \ldots \geq \mu_n$ respectively, then $Trace(A^TB) \leq \sum_{i=1}^n \lambda_i \mu_i$.
For such a natural-looking statement, this was surprisingly hard to prove. However, I finally came up with a proof, and it was cool enough that I felt the need to share. To prove this, we actually need two ingredients. The first is the Cauchy Interlacing Theorem:
Theorem 2: If A is an $n\times n$ symmetric matrix and B is an $(n-k) \times (n-k)$ principle submatrix of A, then $\lambda_{i-k}(A) \leq \lambda_i(B) \leq \lambda_i(A)$, where $\lambda_i(X)$ is the ith largest eigenvalue of X.
Read moreI spent the last several hours trying to come up with an efficient algorithm to the following problem:
Problem: Suppose that we have a sequence of $l$ pairs of non-negative numbers $(a_1,b_1),\ldots,(a_l,b_l)$ such that $\sum_{i=1}^l a_i \leq A$ and $\sum_{i=1}^l b_i \leq B$. Devise an efficient algorithm to find the $k$ pairs $(a_{i_1},b_{i_1}),\ldots,(a_{i_k},b_{i_k})$ that maximize
$\left[\sum_{r=1}^k a_{i_r}\log(a_{i_r}/b_{i_r})\right] + \left[A-\sum_{r=1}^k a_{i_r}\right]\log\left(\frac{A-\sum_{r=1}^k a_{i_r}}{B-\sum_{r=1}^k b_{i_r}}\right).$
Read moreFor collections of independent random variables, the Chernoff bound and related bounds give us very sharp concentration inequalities — if $X_1,\ldots,X_n$ are independent, then their sum has a distribution that decays like $e^{-x^2}$. For random variables that are only pairwise independent, the strongest bound we have is Chebyshev’s inequality, which says that their sum decays like $\frac{1}{x^2}$.
The point of this post is to construct an equality case for Chebyshev: a collection of pairwise independent random variables whose sum does not satisfy the concentration bound of Chernoff, and instead decays like $\frac{1}{x^2}$.
Read more(This post represents research in progress. I may think about these concepts entirely differently a few months from now, but for my own benefit I’m trying to exposit on them in order to force myself to understand them better.)
For many inference tasks, especially ones with either non-linearities or non-convexities, it is common to use particle-based methods such as beam search, particle filters, sequential Monte Carlo, or Markov Chain Monte Carlo. In these methods, we approximate a distribution by a collection of samples from that distribution, then update the samples as new information is added. For instance, in beam search, if we are trying to build up a tree, we might build up a collection of $K$ samples for the left and right subtrees, then look at all $K^2$ ways of combining them into the entire tree, but then downsample again to the $K$ trees with the highest scores. This allows us to search through the exponentially large space of all trees efficiently (albeit at the cost of possibly missing high-scoring trees).
One major problem with such particle-based methods is diversity: the particles will tend to cluster around the highest-scoring mode, rather than exploring multiple local optima if they exist. This can be bad because it makes learning algorithms overly myopic. Another problem, especially in combinatorial domains, is difficulty of partial evaluation: if we have some training data that we are trying to fit to, and we have chosen settings of some, but not all, variables in our model, it can be difficult to know if that setting is on the right track (for instance, it can be difficult to know whether a partially-built tree is a promising candidate or not). For time-series modeling, this isn’t nearly as large of a problem, since we can evaluate against a prefix of the time series to get a good idea (this perhaps explains the success of particle filters in these domains).
Read moreHere’s a fun counterexample: a function $\mathbb{R}^n \to \mathbb{R}$ that is jointly convex in any $n-1$ of the variables, but not in all variables at once. The function is
$f(x_1,\ldots,x_n) = \frac{1}{2}(n-1.5)\sum_{i=1}^n x_i^2 - \sum_{i < j} x_ix_j$
To see why this is, note that the Hessian of $f$ is equal to
$\left[ \begin{array}{cccc} n-1.5 & -1 & \cdots & -1 \\ -1 & n-1.5 & \cdots & -1 \\ \vdots & \vdots & \ddots & \vdots \\ -1 & -1 & \cdots & n-1.5 \end{array} \right]$
This matrix is equal to $(n-0.5)I - J$, where $I$ is the identity matrix and $J$ is the all-ones matrix, which is rank 1 and whose single non-zero eigenvalue is $n$. Therefore, this matrix has $n-1$ eigenvalues of $n-0.5$, as well as a single eigenvalue of $-0.5$, and hence is not positive definite.
On the other hand, any submatrix of size $n-1$ is of the form $(n-0.5)I-J$, but where now $J$ is only $(n-1) \times (n-1)$. This matrix now has $n-2$ eigenvalues of $n-0.5$, together with a single eigenvalue of $0.5$, and hence is positive definite. Therefore, the Hessian is positive definite when restricted to any $n-1$ variables, and hence $f$ is convex in any $n-1$ variables, but not in all $n$ variables jointly.
Read moreAn important concept in online learning and convex optimization is that of strong convexity: a twice-differentiable function $f$ is said to be strongly convex with respect to a norm $\|\cdot\|$ if
$z^T\frac{\partial^2 f}{\partial x^2}z \geq \|z\|^2$
for all $z$ (for functions that are not twice-differentiable, there is an analogous criterion in terms of the Bregman divergence). To check strong convexity, then, we basically need to check a condition on the Hessian, namely that $z^THz \geq \|z\|^2$. So, under what conditions does this hold?
For the $l^2$ norm, the answer is easy: $z^THz \geq \|z\|_2^2$ if and only if $H \succeq I$ (i.e., $H-I$ is positive semidefinite). This can be shown in many ways, perhaps the easiest is by noting that $z^THz-\|z\|_2^2 = z^T(H-I)z$.
For the $l^{\infty}$ norm, the answer is a bit trickier but still not too complicated. Recall that we want necessary and sufficient conditions under which $z^THz \geq \|z\|_{\infty}^2$. Note that this is equivalent to asking that $z^THz \geq (z_i)^2$ for each coordinate $i$ of $z$, which in turn is equivalent to $H \succeq e_ie_i^T$ for each coordinate vector $e_i$ (these are the vectors that are 1 in the $i$th coordinate and 0 everywhere else).
Read moreI’ve decided to branch out a bit from technical discussions and engage in, as Scott Aaronson would call it, some metaphysical spouting. The topic of today is the effective altruism movement. I’m about to be relentlessly critical of it, so this is probably not the best post to read as your first introduction. Instead, read this and this. Then you can read what follows (but keep in mind that there are also many good things about the EA movement that I’m failing to mention here).
Read more[Highlights for the busy: de-bunking standard “Bayes is optimal” arguments; frequentist Solomonoff induction; and a description of the online learning framework.]
Short summary. This essay makes many points, each of which I think is worth reading, but if you are only going to understand one point I think it should be “Myth 5″ below, which describes the online learning framework as a response to the claim that frequentist methods need to make strong modeling assumptions. Among other things, online learning allows me to perform the following remarkable feat: if I’m betting on horses, and I get to place bets after watching other people bet but before seeing which horse wins the race, then I can guarantee that after a relatively small number of races, I will do almost as well overall as the best other person, even if the number of other people is very large (say, 1 billion), and their performance is correlated in complicated ways.
If you’re only going to understand two points, then also read about the frequentist version of Solomonoff induction, which is described in “Myth 6″.
Main article. I’ve already written one essay on Bayesian vs. frequentist statistics. In that essay, I argued for a balanced, pragmatic approach in which we think of the two families of methods as a collection of tools to be used as appropriate. Since I’m currently feeling contrarian, this essay will be far less balanced and will argue explicitly against Bayesian methods and in favor of frequentist methods. I hope this will be forgiven as so much other writing goes in the opposite direction of unabashedly defending Bayes. I should note that this essay is partially inspired by some of Cosma Shalizi’s blog posts, such as this one.
Read moreThere has been much recent discussion about AI risk, meaning specifically the potential pitfalls (both short-term and long-term) that AI with improved capabilities could create for society. Discussants include AI researchers such as Stuart Russell and Eric Horvitz and Tom Dietterich, entrepreneurs such as Elon Musk and Bill Gates, and research institutes such as the Machine Intelligence Research Institute (MIRI) and Future of Humanity Institute (FHI); the director of the latter institute, Nick Bostrom, has even written a bestselling book on this topic. Finally, ten million dollars in funding have been earmarked towards research on ensuring that AI will be safe and beneficial. Given this, I think it would be useful for AI researchers to discuss the nature and extent of risks that might be posed by increasingly capable AI systems, both short-term and long-term. As a PhD student in machine learning and artificial intelligence, this essay will describe my own views on AI risk, in the hopes of encouraging other researchers to detail their thoughts, as well.
Read moreConsider a probability distribution ${p(y)}$ on a space ${\mathcal{Y}}$. Suppose we want to construct a set ${\mathcal{P}}$ of probability distributions on ${\mathcal{Y}}$ such that ${p(y)}$ is the maximum-entropy distribution over ${\mathcal{P}}$:
$\displaystyle H(p) = \max_{q \in \mathcal{P}} H(q), $
where ${H(p) = \mathbb{E}_{p}[-\log p(y)]}$ is the entropy. We call such a set a maximum-entropy set for ${p}$. Furthermore, we would like ${\mathcal{P}}$ to be as large as possible, subject to the constraint that ${\mathcal{P}}$ is convex.
Does such a maximal convex maximum-entropy set ${\mathcal{P}}$ exist? That is, is there some convex set ${\mathcal{P}}$ such that ${p}$ is the maximum-entropy distribution in ${\mathcal{P}}$, and for any ${\mathcal{Q}}$ satisfying the same property, ${\mathcal{Q} \subseteq \mathcal{P}}$? It turns out that the answer is yes, and there is even a simple characterization of ${\mathcal{P}}$:
Read moreSuppose that we have a random variable $X \in \mathbb{R}^d$, such that $\mathbb{E}[XX^{\top}] = I_{d \times d}$. Now take k independent Gaussian random variables $Z_1, \ldots, Z_k \sim \mathcal{N}(0, I_{d \times d})$, and let J be the argmax (over j in 1, …, k) of $Z_j^{\top}X$.
It seems that it should be very hard to predict J well, in the following sense: for any function $q(j \mid x)$, the expectation of $\mathbb{E}_{x}[q(J \mid x)]$, should with high probability be very close to $\frac{1}{k}$ (where the second probability is taken over the randomness in $Z$). In fact, Alex Zhai and I think that the probability of the expectation exceeding $\frac{1}{k}$ should be at most $\exp(-C(\epsilon/k)^2d)$ for some constant C. (We can already show this to be true where we replace $(\epsilon/k)^2$ with $(\epsilon/k)^4$.) I will not sketch a proof here but the idea is pretty cool, it basically uses Lipschitz concentration of Gaussian random variables.
Read moreHere are two strange facts about matrices, which I can prove but not in a satisfying way.
If anyone has insight into either of these, I’d be very interested!
Read moreWhen I meet someone who works in a field outside of computer science, I usually ask them a lot of questions about their field that I’m curious about. (This is still relevant even if I’ve already met someone in that field before, because it gives me an idea of the range of expert consensus; for some questions this ends up being surprisingly variable.) I often find that, as an outsider, I can think of natural-seeming questions that experts in the field haven’t thought about, because their thinking is confined by their field’s paradigm while mine is not (pessimistically, it’s instead constrained by a different paradigm, i.e. computer science).
Usually my questions are pretty naive, and are basically what a computer scientist would think to ask based on their own biases. For instance:
The following explains where I plan to donate in 2016, with some of my thinking behind it. This year, I had \$10,000 to allocate (the sum of my giving from 2015 and 2016, which I lumped together for tax reasons; although I think this was a mistake in retrospect, both due to discount rates and because I could have donated in January and December 2016 and still received the same tax benefits).
To start with the punch line: I plan to give \$4000 to the EA donor lottery, \$2500 to GiveWell for discretionary granting, \$2000 to be held in reserve to fund promising projects, \$500 to GiveDirectly, \$500 to the Carnegie Endowment (earmarked for the Carnegie-Tsinghua Center), and \$500 to the Blue Ribbon Study Panel.
For those interested in donating to any of these: instructions for the EA donor lottery and the Blue Ribbon Study Panel are in the corresponding links above, and you can donate to both GiveWell and GiveDirectly at this page. I am looking in to whether it is possible for small donors to give to the Carnegie Endowment, and will update this page when I find out.
Read moreIn my post on where I plan to donate in 2016, I said that I would set aside \$2000 for funding promising projects that I come across in the next year:
The idea behind the project fund is … [to] give in a low-friction way on scales that are too small for organizations like Open Phil to think about. Moreover, it is likely good for me to develop a habit of evaluating projects I come across and thinking about whether they could benefit from additional money (either because they are funding constrained, or to incentivize an individual who is on the fence about carrying the project out). Finally, if this effort is successful, it is possible that other EAs will start to do this as well, which could magnify the overall impact. I think there is some danger that I will not be able to allocate the \$2000 in the next year, in which case any leftover funds will go to next year’s donor lottery.
In this post I will give some further details about this fund. My primary goal is to give others an idea of what projects I am likely to consider funding, so that anyone who thinks they might be a good fit for this can get in contact with me. (I also expect many of the best opportunities to come from people that I meet in person but don’t necessarily read this blog, so I plan to actively look for projects throughout the year as well.)
I am looking to fund or incentivize projects that meet several of the criteria below:
Read moreMachine learning is very good at optimizing predictions to match an observed signal — for instance, given a dataset of input images and labels of the images (e.g. dog, cat, etc.), machine learning is very good at correctly predicting the label of a new image. However, performance can quickly break down as soon as we care about criteria other than predicting observables. There are several cases where we might care about such criteria:
Consider the following statements:
What do these all have in common? Despite being fairly non-trivial and deep results, they all can be proved in less than half of a page using the Prékopa–Leindler inequality.
(I won’t show this here, or give formal versions of the statements above, but time permitting I will do so in a later blog post.)
Read moreHere is interesting linear algebra fact: let $A$ be an $n \times n$ matrix and $u$ be a vector such that $u^{\top}A = \lambda u^{\top}$. Then for any matrix $B$, $u^{\top}((A-B)(\lambda I - B)^{-1}) = u^{\top}$.
The proof is just basic algebra: $u^{\top}(A-B)(\lambda I - B)^{-1} = (\lambda u^{\top} - u^{\top}B)(\lambda I - B)^{-1} = u^{\top}(\lambda I - B)(\lambda I - B)^{-1} = u^{\top}$.
Why care about this? Let’s imagine that $A$ is a (not necessarily symmetric) stochastic matrix, so $1^{\top}A = 1^{\top}$. Let $A-B$ be a low-rank approximation to $A$ (so $A-B$ consists of all the large singular values, and $B$ consists of all the small singular values). Unfortunately since $A$ is not symmetric, this low-rank approximation doesn’t preserve the eigenvalues of $A$ and so we need not have $1^{\top}(A-B) = 1^{\top}$. The $(I-B)^{-1}$ can be thought of as a “correction” term such that the resulting matrix is still low-rank, but we’ve preserved one of the eigenvectors of $A$.
Read moreIn my previous post, “Latent Variables and Model Mis-specification”, I argued that while machine learning is good at optimizing accuracy on observed signals, it has less to say about correctly inferring the values for unobserved variables in a model. In this post I’d like to focus in on a specific context for this: inverse reinforcement learning (Ng et al. 2000, Abeel et al. 2004, Ziebart et al. 2008, Ho et al 2016), where one observes the actions of an agent and wants to infer the preferences and beliefs that led to those actions. For this post, I am pleased to be joined by Owain Evans, who is an active researcher in this area and has co-authored an online book about building models of agents (see here in particular for a tutorial on inverse reinforcement learning and inverse planning).
Owain and I are particularly interested in inverse reinforcement learning (IRL) because it has been proposed (most notably by Stuart Russell) as a method for learning human values in the context of AI safety; among other things, this would eventually involve learning and correctly implementing human values by artificial agents that are much more powerful, and act with much broader scope, than any humans alive today. While we think that overall IRL is a promising route to consider, we believe that there are also a number of non-obvious pitfalls related to performing IRL with a mis-specified model. The role of IRL in AI safety is to infer human values, which are represented by a reward function or utility function. But crucially, human values (or human reward functions) are never directly observed.
Read moreI’ve spent much of the last few days reading various ICML papers and I find there’s a few pieces of feedback that I give consistently across several papers. I’ve collated some of these below. As a general note, many of these are about local style rather than global structure; I think that good local style probably contributes substantially more to readability than global structure and is in general under-rated. I’m in general pretty willing to break rules about global structure (such as even having a conclusion section in the first place! though this might cause reviewers to look at your paper funny), but not to break local stylistic rules without strong reasons.
General Writing Advice
Suppose that we want to construct subsets $S_1, \ldots, S_m \subseteq \{1,\ldots,n\}$ with the following properties:
| $ | S_i | \geq k$ for all $i$ |
| $ | S_i \cap S_j | \leq 1$ for all $i \neq j$ |
The goal is to construct as large a family of such subsets as possible (i.e., to make $m$ as large as possible). If $k \geq 2\sqrt{n}$, then up to constants it is not hard to show that the optimal number of sets is $\frac{n}{k}$ (that is, the trivial construction with all sets disjoint is essentially the best we can do).
Here I am interested in the case when $k \ll \sqrt{n}$. In this case I claim that we can substantially outperform the trivial construction: we can take $m = \Omega(n^2 / k^3)$. The proof is a very nice application of the asymmetric Lovasz Local Lemma. (Readers can refresh their memory here on what the asymmetric LLL says.)
Read moreIn machine learning, we are obsessed with datasets and metrics: progress in areas as diverse as natural language understanding, object recognition, and reinforcement learning is tracked by numerical scores on agreed-upon benchmarks. Despite this, I think we focus too little on measurement—that is, on ways of extracting data from machine learning models that bears upon important hypotheses. This might sound paradoxical, since benchmarks are after all one way of measuring a model. However, benchmarks are a very narrow form of measurement, and I will argue below that trying to measure pretty much anything you can think of is a good mental move that is heavily underutilized in machine learning. I’ll argue this in three ways:
Each year I aim to donate around 10% of my income. In 2019, I fell behind on this, probably due to the chaos of COVID-19 (but really this was just an embarassing logistical failure on my part). I’ve recently, finally, finished processing donations for 2019 and 2020. In this post I write about my decisions, in case they are useful to others; see also here for a past write-up from 2016.
Read moreResearch ability, like most tasks, is a trainable skill. However, while PhD students and other researchers spend a lot of time doing research, we often don’t spend enough time training our research abilities in order to improve. For many researchers, aside from taking classes and reading papers, most of our training is implicit, through doing research and interacting with mentors (usually a single mentor–our PhD advisor or research manager). By analogy, we are like basketball players who somehow made it to the NBA, and are now hoping that simply playing basketball games will be enough to keep improving.
Drawing on this analogy, I want to talk about two habits that are ubiquitous among elite athletes, that have analogs in research that I feel are underutilized. Those who do pursue these habits as PhD students often improve quickly as researchers.
Read moreThere is a growing fear that algorithmic recommender systems, such as Facebook, Youtube, Netflix, and Amazon, are having negative effects on society, for instance by manipulating users into behaviors that they wouldn’t endorse (e.g. getting them addicted to feeds, leading them to form polarized opinions, recommending false but convincing content).
Some common responses to this fear are to advocate for privacy or to ask that users have greater agency over what they see. I argue below that neither of these will solve the problem, and that the problem may get far worse in the future. I then speculate on alternative solutions based on audits and “information marketplaces”, and discuss their limitations.
Read morePolarization caused by social media is seen by many as an important societal problem, which also overlaps with AI alignment (since social media recommendations come from ML algorithms). I have personally begun directing some of my research to recommender alignment, which has gotten me curious about the extent to which polarization is actually driven by social media. This blog post is the first in a series that summarizes my current take-aways. I’ll start (in this post) by looking at aggregate trends in polarization, then connect them with micro-level data on Facebook feeds in later posts.
I started out feeling that most polarization probably comes from social media. As I read more, my views have shifted: I think there’s pretty good evidence that other sources, including cable news, have historically driven a lot of polarization (see DellaVigna and Kaplan (2006) and Martin and Yurukoglu (2017)), and that we would be highly polarized even without social media. In addition, most readers of this post (and myself) are “extremely online”, and probably intuitively overestimate the impact of social media on a typical American. However, it is possible that social media has further accelerated polarization to an important degree, but the data are too noisy to provide strong evidence either way.
Read moreI’ve switched the host of my blog to Ghost, so my blog is now located at https://bounded-regret.ghost.io/.
Feedly users can subscribe via RSS here. Or click the bottom-right subscribe button on this page to get e-mail notifications of new posts.
Read moreFall 2019
Fall 2020
Spring 2020
Fall 2021
Spring 2021
Spring 2022