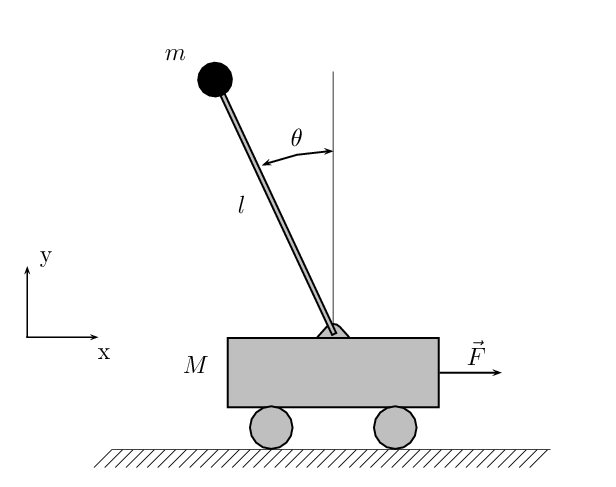
Last time I talked about linear control, I presented a Linear Quadratic Regulator as a general purpose hammer for solving linear control problems. In this post I’m going to explain why LQR by itself is not enough (even for nominally linear systems). (Author’s note: I got to the end of the post and realized I didn’t fulfill my promise in the previous sentence. So it’s redacted, but will hopefully be dealt with in a later post.) Then I’m going to do my best to introduce a lot of the standard ideas in linear control theory.
My motivation for this is that, even though these ideas have a reasonably nice theory from a mathematical standpoint, they are generally presented from an engineering standpoint. And although all of the math is right there, and I’m sure that professional control theorists understand it much better than I do, I found that I had to go to a lot of effort to synthesize a good mathematical explanation of the underlying theory.
However, this effort was not due to any inherent difficulties in the theory itself, but rather, like I said, a disconnect in the intuition of, and issues relevant to, an engineer versus a mathematician. I’m not going to claim that one way of thinking is better than the other, but my way of thinking, and I assume that of most of my audience, falls more in line with the mathematical viewpoint. What’s even better is that many of the techniques built up for control theory have interesting ramifications when considered as statements about vector spaces. I hope that you’ll find the exposition illuminating.
 As before, we will consider a linear system
As before, we will consider a linear system
$\dot{x} = Ax+Bu,$
where $A$ and $B$ are matrices and $u$ is a vector of control inputs ($x$ is the state of the system). However, in addition to a control input $u$, we will have an output $y$, such that $y$ is a function of $x$ and $u$:
$y = Cx+Du.$
In some cases, $y$ will be a set of observed states of a system, but in principal $y$ can be any quantity we care about, provided that it is a linear function of state and control. We further assume that $A$, $B$, $C$, and $D$ are constant with respect to time. We call a system that follows this assumption a linear time-invariant system, or just LTI system.
Since the system is linear, we have superposition and therefore can break up any function (for example, the function from $u(t)$ to $y(t)$) into a function from each coordinate of $u(t)$ to each coordinate of $y(t)$. For each of these functions, we can take their Laplace transform. So, we start with
$\dot{x} = Ax+Bu$
$y = Cx+Du$
and end up with (after taking the Laplace transform)
$sX = AX+BU$
$Y = CX+DU.$
Solving these two equations for $Y$ as a function of $U$ gives $Y = (C(sI-A)^{-1}B+D)U$. We call this mapping from $U$ to $Y$ the transfer function of the system. Cramer’s Rule implies that the transfer function of any linear time-invariant system will be a matrix where each entry is a ratio of two polynomials. We refer to such transfer functions as rational. I will show later that the converse is also true: any rational matrix is the transfer function of some LTI system. We call such an LTI system the state-space representation of the transfer function. (I apologize for throwing all this terminology at you, but it is used pretty unapologetically in control systems literature so I’d feel bad leaving it out.)
As an example, consider a damped harmonic oscillator with an external force $u$ as a control input, and suppose that the outputs we care about are position and velocity. We will let $q$ denote the position of the oscillator. This has the following state-space representation:
$\left[ \begin{array}{c} \dot{q} \\ \ddot{q} \end{array} \right] = \left[ \begin{array}{cc} 0 & 1 \\ -k & -b \end{array} \right] \left[ \begin{array}{c} q \\ \dot{q} \end{array} \right] + \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] u$
$\left[ \begin{array}{c} y_1 \\ y_2 \end{array} \right] = \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right] \left[ \begin{array}{c} q \\ \dot{q} \end{array} \right] + 0 \cdot u$
Here $k$ is the spring constant of the oscillator and $b$ is the damping factor. For convenience we will write $x$ instead of $\left[ \begin{array}{c} q \\ \dot{q} \end{array} \right]$ and $y$ instead of $\left[ \begin{array}{c} y_1 \\ y_2 \end{array} \right]$. Also, we will let $I$ denote the $2 \times 2$ identity matrix. Then, after taking the Laplace transform, we get
$sX = \left[ \begin{array}{cc} 0 & 1 \\ -k & -b \end{array} \right]X + \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]U$
$Y = X.$
Solving the first equation gives
$\left[ \begin{array}{cc} s & -1 \\ k & s+b \end{array} \right] X = \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]U,$
or
$X = \frac{1}{s^2+bs+k}\left[ \begin{array}{cc} s+b & 1 \\ -k & s \end{array} \right]\left[ \begin{array}{c} 0 \\ 1 \end{array}\right]U = \frac{1}{s^2+bs+k} \left[ \begin{array}{c} 1 \\ s \end{array} \right]U$
Therefore, the transfer function from $U$ to $Y$ is $\frac{1}{s^2+bs+k} \left[ \begin{array}{c} 1 \\ s \end{array} \right]$.
We can think of the transfer function as a multiplier on the frequency spectrum of $u$ (note that $s$ is allowed to be an arbitrary complex number; if $s$ is non-real then we have oscillation at a frequency equal to the imaginary part of $s$; if $\Re(s) < 0$ then we have damped oscillation, whereas if $\Re(s) > 0$ then the magnitude of the oscillation increases exponentially. Note that $\Re(s)$ denotes the real part of $s$.
Exercise: What does a pole of a transfer function correspond to? What about a zero? Answers below the fold.
 If a transfer function has a pole, then it means that even if a given frequency doesn’t show up in the input $u$, it can still show up in the output $y$. Thus it is some self-sustaining, natural mode of the system. For LTI systems, this corresponds to an eigenvector of the matrix $A$, and the location of the pole is the corresponding eigenvalue.
If a transfer function has a pole, then it means that even if a given frequency doesn’t show up in the input $u$, it can still show up in the output $y$. Thus it is some self-sustaining, natural mode of the system. For LTI systems, this corresponds to an eigenvector of the matrix $A$, and the location of the pole is the corresponding eigenvalue.
A zero, on the other hand, means that a mode will not show up in the output even if it is present in the input. So for instance, the damped oscillator has poles at $\frac{-b \pm \sqrt{b^2-4k}}{2}$. Let us assume that $b$ and $k$ are both positive for the damped oscillator. Then, for $b \geq 2\sqrt{k}$, both of the poles are real and negative, meaning that the system is critically damped. For $b < 2\sqrt{k}$, the poles have negative real part and imaginary part equal to $\sqrt{k-\frac{b^2}{4}}$, meaning that the system will exhibit damped oscillation. Finally, there is a zero in the second coordinate of the transfer matrix at $s = 0$. This corresponds to the fact that a harmonic oscillator can be held at a fixed distance from its natural fixed point by a fixed external force. Since the distance is fixed, the contribution to velocity is zero.
There is more to be said on transfer functions, but before I go into that I would like to give you a working picture of how $u$ and $y$ should be viewed mathematically. This is a view that I only recently acquired. For this I owe thanks to Stefano Stramigioli, who gave a very interesting talk on port-Hamiltonian methods at Dynamic Walking 2010. (Update: Stefano recommends this book as a resource for learning more.)
Duality
Here is how I think you should think about linear control mathematically. First, you have a state-space $V$. You also have a space of controls $U$ and a space of outputs $Y$. Finally, you have a space $TV$, the tangent space to $V$.
Ignoring $U$ and $Y$ for a moment, let’s just focus on $V$ and $TV$. We can think of elements of $TV$ as generalized forces, and the elements of $V$ as generalized velocities. I realize that state-space also takes position into account, but you will note that no external forces show up in the equations for position, so I think this view still makes sense.
If we have a set of forces and velocities, then we can compute power (if our system is in regular Cartesian coordinates, then this is just $\vec{F} \cdot \vec{v}$). In this way, we can think of $V$ and $TV$ as dual to each other. I think that generalized velocities are actually somehow supposed to live in the cotangent space $T^*V$, rather than $V$, but I don’t know enough analysis to see why this is true. If someone else does, I would love to hear your explanation.
At any rate, we have these two spaces, $V$ and $TV$, that are in duality with each other. The operator $A : V \to TV$ then induces a map $\tilde{A}$ from $\mathcal{L}^{1}(\mathbb{R},TV)$ to $\mathcal{L}^{1}(\mathbb{R},V)$, where $\mathcal{L}^{1}(X,Y)$ is the space of Lesbegue-integrable functions from $X$ to $Y$ (although in practice all of our inputs and outputs will be real-valued, not complex-valued, since the systems we care about are all physical). Since $V$ and $TV$ are in duality with each other, we can also think of this as assigning a power history to any force history (the power history being $[\tilde{A}(f)](f)$, where $f$ is the force history).
What’s more remarkable is that the transfer function from force histories to state histories is $(sI-A)^{-1}$ in the Laplace domain (as discussed above – just set $B = C = I$ for the state-space representation). Therefore it is invertible except on a set of measure zero (the poles of $A$) and so as far as $\mathcal{L}^{1}$ spaces are concerned it is an isomorphism; this is a bit of a technical point here, but I’m using the fact that $\mathcal{L}^1$ spaces are composed of equivalence classes of functions that differ on sets of measure zero, and also probably implicitly using some theorems from Fourier analysis about how the Fourier (Laplace) transform is an isomorphism from $\mathcal{L}^{1}(\mathbb{R},V)$ to itself. I’m still glossing over some technical details here; in particular, I think you might need to consider the intersection of $\mathcal{L}^1$ and $\mathcal{L}^2$ instead of just $\mathcal{L}^1$, and also the target space of the Fourier transform is really $\mathcal{L}^{1}(\widehat{\mathbb{R}},V)$, not $\mathcal{L}^1(\mathbb{R},V)$, but these details aren’t really important to the exposition.
Getting back on track, we’ve just shown that the dynamics matrix $A$ of a linear system induces an isomorphism between force histories and state histories. My guess is that you can also show this for reasonably nice non-linear systems, but I don’t have a proof off the top of my head. So, letting $U$ denote the space of control signals and $Y$ the space of outputs, what we have is something like this:
$\mathcal{L}^{1}(\mathbb{R},U) \xrightarrow{B} \mathcal{L}^{1}(\mathbb{R},TV) \xrightarrow{\overset{\tilde{A}}{\sim}} \mathcal{L}^{1}(\mathbb{R},V) \xrightarrow{C} \mathcal{L}^{1}(\mathbb{R},Y)$
Incidentally, that middle map (the isomorphism with $\tilde{A}$) is hideous-looking, and if someone has a good way to typeset such a thing I would like to know about it.
In any case, in this context it is pretty easy to see how the inputs and outputs play dual roles to each other, and in fact if we replaced $A$, $B$, and $C$ each with their adjoints $A^{\dagger}$, $B^{\dagger}$, and $C^{\dagger}$, then we get a new dynamical system where the inputs and outputs actually switch places (as well as the matrices governing the inputs and outputs). Note that I’ve left $D$ out of this for now. I’m not really sure yet of a good way to fit it into this picture; it’s possible that $D$ is just unnatural mathematically but sometimes necessary physically (although usually we can assume that $D = 0$).
Now that we have this nice framework for thinking about linear control systems, I’m going to introduce controllers and observers, and it will be easy to see that they are dual to each other in the sense just described.
Controllability and Observability
Go back to the non-linear case for a moment and suppose that we have a system $\dot{x} = f(x,u)$, or, in the notation I’ve been using, $\dot{x} = f(x) + Bu$. We say that such a system is controllable if for any two states $x_1$ and $x_2$, there exists a time $t_0 > 0$ and a control signal $u(t)$ such that if $x(0) = x_1$ then $x(t_0) = x_2$ when the system is driven by the control signal $u(t)$. What this says intuitively is that we can get from any state to any other state in a finite amount of time.
For linear systems, controllability implies something stronger — we can actually get from any state to any other state arbitrarily quickly, and this is often times the definition given in the linear case. For non-linear systems, this is not the case, as a trivial example we could have
$\dot{x_1} = u$
$\dot{x_2} = max(x_1,1)$
There are a few important properties of linear systems that are equivalent to controllability:
(1) There is no proper subspace $W$ of the state space such that $A(W) \subset W$ and $B(U) \subset W$, where $U$ is the space of possible instantaneous control signals. The intuition is that there is no subspace that the passive dynamics (without control) can get stuck in such that the control input can’t move the dynamics out of that space.
(2) There is no left eigenvector of $A$ that is in the left null space of $B$. In other words, it actually suffices to check the criterion (1) above just for one-dimensional subspaces.
(3) The matrix $[B \ AB \ A^2B \ \ldots \ A^{n-1}B]$, where $n$ is the dimension of the state space of the system, has full row rank.
(4) For any choice of $n$ eigenvalues $\lambda_1, \ldots, \lambda_n$, there exists a matrix $F$ such that $A+BF$ has generalized eigenvalues $\lambda_1, \ldots, \lambda_n$. We can think of this as saying that an appropriate linear feedback law $u = Fx$ can be used to give the closed-loop (i.e. after control is applied) dynamics arbitrary eigenvalues.
I will leave (1) and (2) to you as exercises. Note that this is because I actually think you can solve them, not because I’m being lazy. (3) I will prove shortly (it is a very useful computational criterion for testing controllability). (4) I will prove later in this post. I should also note that these criteria also hold for a discrete-time system
$x_{n+1} = Ax_n + Bu_n$
$y_n = Cx_n + Du_n$
Proof of (3): In the case of a discrete-time system, if we have control inputs $u_1, \ldots, u_k$, then $x_{k+1}$ will be
$A^k x_1 + (Bu_k + ABu_{k-1} + A^2Bu_{k-2} + \ldots + A^{k-1}Bu_1)$
In particular, after $k$ time steps we can affect $x_{k+1}$ by an arbitrary linear combination of elements from the row spaces of $A^{i}B$, where $i$ ranges from $0$ to $k-1$. In other words, we can drive $x_{k+1}$ to an arbitrary state if and only if the row space of $[A^{i}B]_{i=0}^{k-1}$ is the entire state space, i.e. $[A^{i}B]_{i=0}^{k-1}$ has full row rank. So a discrete-time system is controllable if and only if $[A^{i}B]_{i=0}^{k-1}$ has full row rank for some sufficiently large $k$.
To finish the discrete-time case, we use the Cayley-Hamilton theorem, which shows that any $n \times n$ matrix satisfies a degree $n$ polynomial, and so in particular it suffices to pick $k = n$ above, since $A^nB$ can be written as a linear combination of $A^{i}B$ for $i < n$, and similarly for any larger powers of $A$.
Now we need to deal with the continuous time case. In this case, we can use the theory of linear differential equations to show that
$x(t) = x(0)e^{At} + \int_{0}^{t} e^{A\tau}Bu(t-\tau) d\tau,$
where $e^{A\tau}$ is the matrix exponential of $A\tau$. But if we use the Cayley-Hamilton theorem a second time, we see that $e^{A\tau}$ can be expressed as an $(n-1)$st degree polynomial in $A\tau$, so that there exists some $c_0(\tau), \ldots, c_{n-1}(\tau)$ such that
$x(t) =e^{At}x(0) + \sum_{k=0}^{n-1} A^kB \int_{0}^{t} c_k(\tau)u(t-\tau) d\tau.$
From here it is clear that, in order for a continuous time system to be controllable, the controllability matrix must have full row rank (since $x(t)$ is equal to $e^{At}x(0)$ plus something in the row space of the controllability matrix). The converse is less obvious. If the $c_k(\tau)$ were linearly independent functions, then we would be done, because the last term in the sum can be thought of as the inner product of $c_k(\tau)$ and $u(t-\tau)$, and we can just use Gram-Schmidt orthogonalization to show that those inner products can be chosen arbitrarily (if you don’t see this then figuring it out is a good linear algebra exercise).
The problem is that the $c_k(\tau)$ are not necessarily linearly independent. If $A$ has all distinct eigenvalues, then they will be. This is because we have the relations $e^{At}v = e^{\lambda t} v$ and $A^k v = \lambda^k v$ for any $\lambda$-eigenvector $v$ of $A$, so we can write $n$ distinct exponential functions as a linear combination of the $c_k(\tau)$, and any relation among the $c_k$ would imply a relation among the $e_{\lambda t}$, which is impossible (it is a basic result from Fourier analysis that exponential functions are linearly independent).
However, this result actually needs $A$ to have distinct eigenvalues. In particular, if one takes $A = I$, the $n \times n$ identity matrix, then you can show that all but one of the $c_k$ can be chosen arbitrarily. This is because $I$, $I^2$, $\ldots$ are all equal to each other, and thus linearly dependent.
What we need to do instead is let $m$ be the degree of the minimal polynomial $p$ such that $p(A) = 0$. Then we can actually write $e^{At}$ as $\sum_{k=0}^{m-1} d_k(t)$ for some functions $d$:
$\sum_{k=0}^{m-1} d_k(t)A^k = e^{At}$
By the way in which the $d_k$ were constructed (by applying polynomial relations to an absolutely convergent Taylor series), we know that they are all infinitely differentiable, hence we can differentiate both sides $l$ times and write
$\sum_{k=0}^{m-1} d_k^{(l)}(t) A^k = A^l e^{At}$
Now look at these derivatives from $l = 0$ to $l = m-1$. If the $d_k(t)$ were linearly dependent, their derivatives would satisfy the same relation, and therefore (by evaluating everything at $t = 0$, the matrices $A^0, A^1, \ldots, A^{m-1}$ would satisfy a linear relation, which is impossible, since then $A$ would satisfy a polynomial relation of degree less than $m$.
So, the $d_k(t)$ are linearly independent, and thus by the argument with Gram-Schmidt above we can write anything in the row space of $B, AB, \ldots, A^{m-1}B$ as
$e^{At}x(0) + \sum_{k=0}^{m-1} A^kB \int_{0}^{t} d_k(\tau)u(t-\tau) d\tau$
for any $t > 0$. So are we done? Almost. The last step we need to finish is to note that if $A$ satisfies a polynomial of degree $m$ then the row space of $[B \ AB \ \ldots \ A^{m-1}B]$ is the same as the row space of $[B \ AB \ \ldots \ A^{n-1}B]$, for $n > m$.
So, that proves the result (3) about the controllability matrix. It was a lot of work in the continuous time case, although it matches our intuition for why it should be true (taking an exponential and taking a derivative are somewhat complementary to each other, so it made sense to do so; and I think there are probably results in analysis that make this connection precise and explain why we should get the controllability result in the continuous case more or less for free).
As I said before, (4) will have to wait until later.
In addition to controllability, we have a notion of stabilizability, which means that we can influence all unstable modes of $A$. In other words, we can make sure that the system eventually converges to the origin (although not necessarily in finite time). Versions of criteria (2) and (4) exist for stabilizable systems. Criterion (2) becomes a requirement that no left eigenvector of $A$ whose eigenvalue has non-negative real part is in the left null space of $B$. Criterion (4) becomes a requirement that there exist $F$ such that $A+BF$ has only eigenvalues with negative real part.
Observers
We say that a system is observable if, for any initial state $x(0)$ and any control tape $u(t)$, it is possible in finite time to infer $x(0)$ given only $u(t)$ and the output $y(t)$. In particular, we are not given any information about the internal states $x(t)$ of the system (except through $y(t)$), although it is assumed that $A$, $B$, $C$, and $D$ are known. If we have a non-linear system
$\dot{x} = f(x,u)$
$y = g(x,u)$
then it is assumed that $f$ and $g$ are known.
It turns out that observability for a system is exactly the same as controllability for the dual system, so all the criteria from the previous section hold in a suitably dual form. One thing worth thinking about is why these results still hold for any control tape $u(t)$.
(1) There is no non-zero subspace $W$ of $V$ such that $A(W) \subset W$ and $C(W) = 0$. In other words, there is no space that doesn’t show up in the output and such that the natural dynamics of the system stay in that space.
(2) There is no right eigenvector of $A$ that is in the right null space of $C$.
(3) The matrix $\left[ \begin{array}{c} C \\ CA \\ CA^2 \\ \vdots \\ CA^{n-1} \end{array} \right]$ has full column rank.
(4) The eigenvalues of $A+LC$ can be assigned arbitrarily by an appropriate choice of $L$.
Just as the matrix $F$ from the previous section can be thought of as a linear feedback law that gives the system arbitrary eigenvalues, the matrix $L$ is part of a feedback law for something called a Luenburger observer.
Also, just as there is stabilizability for a system, meaning that we can control all of the unstable modes, there is also detectability, which means that we can detect all of the unstable modes.
Luenburger Observers
An observer is a process that estimates the state of an observable system given information about its outputs. If a system is detectable, and $L$ is such that $A+LC$ has only eigenvalues with negative real part, then consider the system
$\dot{q} = Aq+Bu+L(Cq+Du-y)$
Using the fact that $Du-y = -Cx$, we see that
$\dot{(q-x)} = (A+LC)(q-x)$, so that $q-x$ decays exponentially to zero (by the assumption on the eigenvalues of $A+LC$. Thus the dynamical system above, which is called a Luenburger observer, will asymptotically approach the true state of a system given arbitrary initial conditions.
If a system is both controllable and observable, can we design an observer and a controller that working together successfully control the system? (This question is non-trivial because the controller has to use the estimated state from the controller, rather than the actual state of the system, for feedback.) The answer is no in general, but it is yes for linear systems.
Let $F$ be such that $A+BF$ is stable and let $L$ be such that $A+LC$ is stable. (A matrix is stable if all of its eigenvalues have negative real part.) Now we will consider the system obtained by using $L$ as a Luenburger observer and $F$ as a linear feedback law. Let $e := q-x$. Then we have
$\dot{e} = (A+LC)e$
$\dot{x} = Ax+BFq = (A+BF)x + BFe$
In matrix form, this gives
$\left[ \begin{array}{c} \dot{e} \\ \dot{x} \end{array} \right] = \left[ \begin{array}{cc} A+LC & 0 \\ BF & A+BF \end{array} \right] \left[ \begin{array}{c} e \\ x \end{array} \right].$
Because of the block triangular form of the matrix, we can see that its eigenvalues are given by the eigenvalues of $A+LC$ and $A+BF$. Since $A+LC$ and $A+BF$ are both stable, so is the matrix given above, so we can successfully stabilize the above system to the origin. Of course, this is weaker than full controllability. However, if we have full controllability and observability, then we can set the eigenvalues of the above matrix arbitrarily, which should imply full controllability (I haven’t sat down and proved this rigorously, though).
So, now we know how to stabilize a linear system if it is detectable and stabilizable. The main thing to take away from this is the fact that the poles of the coupled dynamics of state and observation error are exactly the eigenvalues of $A+BF$ and $A+LC$ considered individually.
State-space representations
The final topic I’d like to talk about in this post is state-space representations of transfer functions. It is here that I will prove all of the results that I promised to take care of later. There are plenty more topics in linear control theory, but I’ve been writing this post for a few days now and it’s at a good stopping point, so I’ll leave the rest of the topics for a later post.
A state-space representation of a transfer function is exactly what it sounds like. Given a transfer function $P(s)$ from $U$ to $Y$, find a state-space model
$\dot{x} = f(x,u)$
$y = g(x,u)$
that has $P$ as a transfer function. We’ll be concerned with linear state-space representations only.
The first thing to note is that a linear state-space representation of $P(s)$ can always be reduced to a smaller representation unless the representation is both controllable and observable (by just restricting to the controllable and observable subspace).
The next thing to note is that, since the transfer function of a state-space representation is $C(sI-A)^{-1}B+D$, a transfer function $P(s)$ has an irreducible (in the sense of the preceding paragraph) linear state-space representation of degree $n$ if and only if $P(s) = \frac{q(s)}{r(s)}$, where $q$ and $r$ are polynomials with $\deg(q) \leq \deg(r) = n$. Thus all controllable and observable linear state-space representations of $P(s)$ have the same dimension, and therefore there exists some non-canonical vector space isomorphism such that we can think of any two such representations as living in the same state space (though possibly with different matrices $A$, $B$, $C$, and $D$).
Finally, if two state-space representations over the same vector space have the same transfer function, then one can be obtained from the other by a chance of coordinates. I will now make this more precise and also prove it.
Claim: Suppose that $R_1$ and $R_2$ are two (not necessarily linear) state-space representations with the same input-output mapping. If $R_1$ is controllable and $R_2$ is observable, then there is a canonical map from the state space of $R_1$ to the state space of $R_2$. If $R_1$ is observable, then this map is injective. If $R_2$ is controllable, then this map is surjective. If $R_1$ and $R_2$ are both linear representations, then the map is linear.
Proof: Let the two representations be $\dot{x_1} = f_1(x_1,u), y_1 = g_1(x_1,u)$ and $\dot{x_2} = f_2(x_2,u), y_2 = g_2(x_2,u)$.
Since $R_1$ is controllable, we can take an input tape that sends $x_1$ to an arbitrary state $x$ at some time $t_0$. Then by looking at $y_2$ evolve under the same input tape, by the observability of $R_2$ we will eventually be able to determine $x_2(t_0)$ uniquely. The canonical map sends the $x$ we chose to $x_2(t_0)$.The fact that $y_1(t) = y_2(t)$ for all $t$ guarantees that $x_2(t_0)$ is well-defined (i.e., it doesn’t matter what $u$ we choose to get there).
If $R_2$ is controllable, then we can choose a $u$ that causes us to end up with whatever $x_2(t_0)$ we choose, which implies that the map is surjective. Now for the purposes of actually computing the map, we can always assume that the control input becomes $0$ once we get to the desired $x_1(t_0)$. Then there is a one-to-one correspondence between possible output tapes after time $t_0$ and possible values of $x_2(t_0)$. If $R_1$ is observable, this is also true for $x_1(t_0)$, which implies injectivity. I will leave it to you to verify that the map is linear if both representations are linear.
Finally, I would like to introduce a special case of controllable canonical form and use it to prove criterion (4) about controllability. It will also show, at least in a special case, that any transfer function that is a quotient of two polynomials (where the denominator has at least as high degree as the numerator) has a linear state-space representation.
The special case is when $U$ is one-dimensional. Then our transfer matrix can be written in the form
$p(s) = \frac{\vec{c_1}s^{n-1}+\vec{c_2}s^{n-2}+\ldots+\vec{c_n}}{s^n+a_1s^{n-1}+\ldots+a_n}+\vec{d}$
It turns out that this transfer function can be represented by the following transfer matrix:
$A = \left[ \begin{array}{ccccc} -a_1 & -a_2 & \ldots & -a_{n-1} & -a_n \\ 1 & 0 & \ldots & 0 & 0 \\ 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \ldots & \vdots & \vdots \\ 0 & 0 & \ldots & 1 & 0 \end{array} \right], B = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{array} \right]$
$C = \left[ \begin{array}{ccccc} \vec{c_1} & \vec{c_2} & \cdots & \vec{c_{n-1}} & \vec{c_n} \end{array} \right], D = \vec{d}$
This might seem a bit contrived, but the construction for $A$ is a nice trick for constructing a matrix with a given characteristic polynomial. Also note that $A$ will have a single Jordan block for each distinct eigenvalue (whose size is the number of times that eigenvalue appears in the list $\lambda_1, \ldots, \lambda_n$). One can show directly that this is a necessary and sufficient condition for being controllable by a single input.
I will leave it to you to check the details that the above state-space model actually has $P(s)$ as a transfer function. (Bonus question: what is the equivalent observable canonical form for observable single-output systems?) I will wrap up this post by proving criterion (4) about controllability, as promised. I have reproduced it below for convenience:
(4) An LTI system is controllable if and only if we can assign the eigenvalues of $A+BF$ arbitrarily by a suitable choice of $F$.
Proof: I will prove the “only if” direction, since that is the difficult direction. First consider the case when we have a single-input system. Then take the transfer function from $u$ to $x$ (this is the same as assuming that $C = I$, $D = 0$). By the result above and the assumption of controllability, there exists a system with the same transfer function in controllable canonical form, and thus there is a change of coordinates that puts our system in controllable canonical form. Once we are in canonical form, it is easy to see that by choosing $F = \left[ \begin{array}{ccccc} -b_1 & -b_2 & \ldots & -b_{n-1} & -b_n \end{array} \right]$, we end up with a system whose characteristic polynomial is $\lambda^n + (a_1+b_1)\lambda^{n-1} + \ldots + (a_{n-1}+b_{n-1})\lambda + (a_n+b_n)$. We can therefore give $A+BF$ an arbitrary characteristic polynomial, and thus choose its eigenvalues arbitrarily.
This proves the desired result in the case when we have a single input to our system. When we have multiple inputs, we have to consider them one-by-one, and use the fact that linear feedback can’t affect the eigenvalues of the parts of the system that are outside the controllable subspace. I haven’t checked this approach very carefully, so it might not work, but I am pretty sure it can be made to work. If you want more details, feel free to ask me and I will provide them. At this point, though, I’m writing more of a treatise than a blog post, so I really think I should cut myself off here. I hope the exposition hasn’t suffered at all from this, but if it has, feel free to call me on it and I will clarify myself.
My next post will take a break from linear control and tell you why using least squares is one of the worst ideas ever (because you think it will work when it actually won’t; if you don’t believe me I’ll show you how negligible sampling errors can easily cause you to be off by 10 percent in your model parameters).
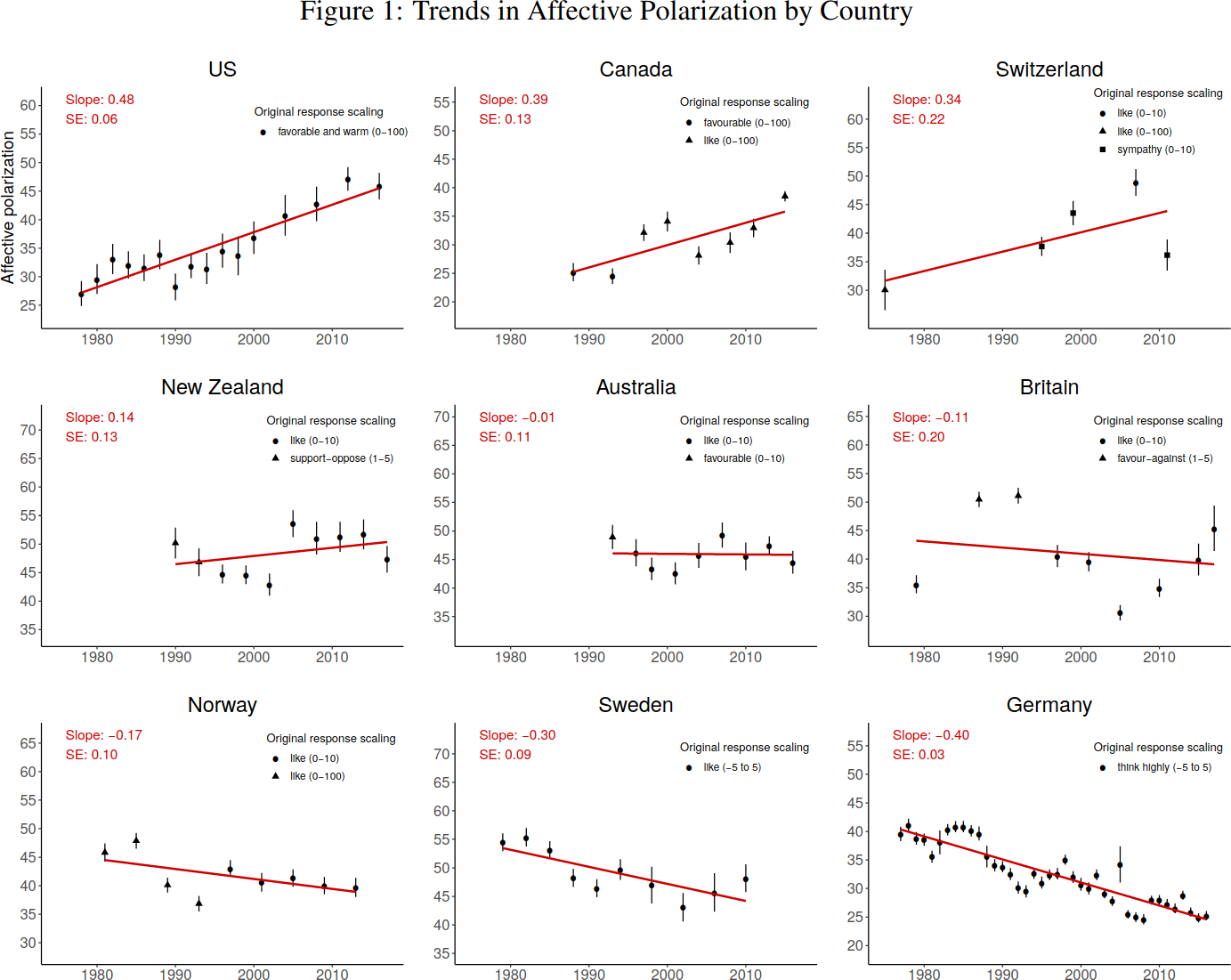
]]>
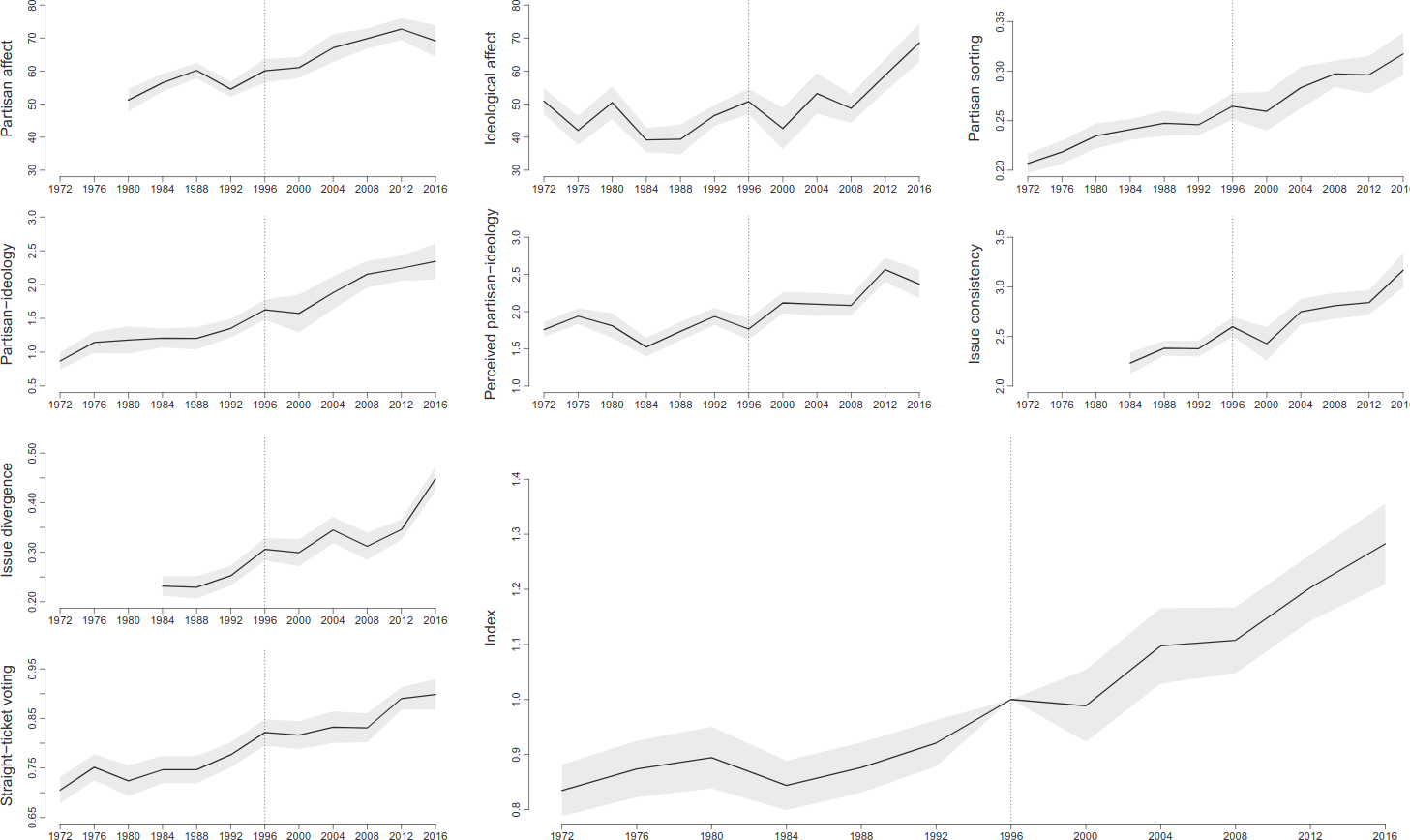






 As before, we will consider a linear system
As before, we will consider a linear system